Clinical trial design

Summary

A major factor in the rapid advancement of the field of cardiovascular medicine in recent years has been the refinement in clinical research methodology and thorough evaluation of new technology. In many ways, interventional cardiology has led the way in translational clinical research, in a constant effort to improve technology and patient outcomes with its multitude of high quality clinical trials forming the basis for evidence-based medical practice and informing practice guidelines.

Investigator-initiated clinical trials, particularly those that compare treatment strategies, may be particularly important to define comparative effectiveness for medical decision making. Universal standards of trial design apply to all clinical trials in order to obtain sound data to inform practice.

In this chapter, we review some of the principles of clinical trial design and implementation, illustrating these with examples from recent trials in interventional cardiology.

Introduction

In the United States, the Food and Drug Administration (FDA) regulates the market approval of new interventional medical devices based on scientific evidence that there is reasonable assurance that the medical device is both safe and effective. This Pre-Market Approval (PMA) is the most stringent type of device marketing application required by the FDA and the approval is based on a determination by the FDA that the PMA contains “sufficient valid scientific evidence to assure that the device is safe and effective for its intended use(s)” [11. Chen E, Sapirstein W, Ahn C, Swain J, Zuckerman B. FDA perspective on clinical trial design for cardiovascular devices. Ann Thorac Surg. 2006;82:773-5. ]. While the FDA emphasises the need for randomised controlled trials (RCTs) for medical treatment approval (drugs and devices), valid scientific evidence may also be obtained from partially controlled studies, trials without matched controls, or observational studies. The level of evidence required may vary according to the characteristics of the device, the target population, the conditions of use, the existence of potential warnings and other restrictions, and the extent of experience with its use.

There are many differences between the approach taken to reviewing and approving new medical devices in Europe and the US [22. Davis S, Gilbertson E, Goodall S. EU medical device approval safety assessment. A comparative analysis of medical device recalls 2005-2009. 2011; Accessed May 11, 2011. http://www. eucomed. org/uploads/Press%20Releases/BCG%20study%20report.
pdf]. The centralised approach to medical device approvals the FDA has taken is fundamentally different from the decentralised model the European Community (EC) has implemented with a significant impact on the approval process, requirements and timing. The current European Union (EU) system is governed by three EC directives. Guidelines for approval are laid out in these EC directives, but the actual approval systems are coordinated at country level. Each country’s competent authority certifies for-profit “Notified Bodies”, standards organisations that are authorised to approve a variety of goods for the EU market and grant a CE (from the French, “Conformité Européene”) mark certification. Among the current Notified Bodies, there are actually 74 separate entities across 25 countries with the authorisation to approve medical devices for the EU market. A manufacturer seeking to market a new medical device in the EU must select one of these Notified Bodies to certify the new device applications with the CE mark. Based upon the device classification, the Notified Body will request certain materials (e.g., a literature review or clinical data) and perform manufacturing quality assessments on the manufacturing process. This clinical data (which includes data from bench testing to clinical trials in human subjects) used for CE marking may be in one of two forms: either a compilation of the relevant scientific literature currently available on the intended purpose of the device and the techniques employed, or, if appropriate, a report containing a critical evaluation of the compilation of the results and conclusions of a specifically designed clinical investigation. Upon satisfactory review and approval, a CE mark is awarded, enabling access to the entire EU market.

The requirements for market entry in Asia vary greatly across countries, with some countries just beginning to establish regulatory oversight and others with well-developed systems for market application. In Japan, the Pharmaceuticals and Medical Devices Agency (PMDA) works together with the Ministry of Health, Labour and Welfare (MHLW) to review marketing authorisation applications for medical devices. The State Food and Drug Administration (SFDA) and local subsidiaries are responsible for the regulation and management of medical devices in China.

Types of clinical trials

A clinical trial may be defined as a form of planned experiment involving human subjects for the evaluation of a therapeutic intervention. As opposed to observational cohort studies, in clinical trials treatment is initiated by the investigators according to a specific plan for its evaluation.

The 3 most common types of clinical trial are uncontrolled clinical trials, non-randomised controlled trials and randomised clinical trials (RCT). In uncontrolled clinical trials, no concurrent comparison group exists. In non-randomised controlled trials, a control comparison group exists but the treatment allocation to the study arms is not by a randomised process. By contrast, in RCT the treatment is randomly assigned to the participants resulting in a standard or control treatment group and one or more experimental groups. Arguably, a randomised clinical trial is the gold standard scientific method for evaluating treatment interventions and forms the basis of evidence-based medical practice.

Types of clinical trial may also be classified according to the objective of the study. Typically, this involves classification into 4 phases ( Table 1 ). Phase 1 studies are primarily concerned with evaluation of drug or device safety. They may be performed on normal human volunteers if the treatment is expected to be relatively low risk or on patients with advanced disease if high risk. Phase 1 studies may include dose escalation experiments in which the participant is exposed to increasing doses of a drug or graded treatment according to a predefined algorithm. Phase 2 trials are small studies to determine whether the new intervention is efficacious and not associated with prohibitive risk. These studies often use surrogates or biomarkers to screen interventions that warrant further study in a larger trial. After a therapy has been shown to be reasonably effective in Phase 2 trials, a Phase 3 clinical trial is conducted to compare the new treatment to the current standard of care, or placebo control if a standard does not exist. Generally, Phase 3 trials are RCTs with clinical endpoints. The results of these trials may result in a drug or therapy being approved for marketing. After licensing, Phase 4 trials may be undertaken to document long-term adverse events that may have been too infrequent to be evaluated in Phase 3 trials. While progression from Phase 1 to Phase 3 has been the norm, it is not always the case: combined Phase 1/2 trials and Phase 2/3 trials are not uncommon.

Bias and confounding

Bias is a source of variation due to systematic error in the design, conduct or analysis of a study leading to a result that differs from the underlying truth. Some examples of bias include selection bias, which refers to systematic differences between comparison groups in prognosis or responsiveness to treatment, misclassification bias where patients are incorrectly categorised with regard to either exposure or outcome, and recall bias where subjects who have experienced an outcome have a different likelihood of recalling events (exposures) compared to those who have not suffered an adverse event.

Confounders are factors that are related to both the exposure of interest and the outcome of the study and obscure the true relationship between the exposure of interest and outcome, making this association either weaker or stronger than in truth. For example, hypertension is a confounder when considering the association between obesity (exposure) and mortality (outcome). Both bias and confounders are a threat to the internal validity of a study and need to be addressed in trial design, implementation and analysis.

Protocol document

A study protocol, a formal document explaining how the study will be conducted, is an essential component of a clinical trial. Table 2 outlines the common components of a clinical trial study protocol. It addresses the 4 fundamental aspects of trial design at the outset:

1. which patients are eligible for the study,
2. the treatments being evaluated and the hypothesis of the study,
3. what endpoints are going to be studied and how patients will be followed up, and
4. the planned statistical analysis.

Concept of equipoise

Equipoise refers to an ethical concept in the design and conduct of clinical trials. Broadly speaking, it is only ethical to conduct clinical trials in areas of uncertainty. There are two conditions that need to be satisfied for equipoise to exist: 1) there is no evidence to suggest that any treatment or therapy in the trial is better than another, and 2) there is no evidence to suggest that there is any therapy (external to the trial) that is better than the treatments being evaluated in the trial. Thus, it is unethical to initiate a RCT if it does not include the “standard” therapy as one of the treatment arms if standard therapy exists, or to use a study arm known to be inferior to any other treatment as a comparator.

Randomised clinical trials

There are many examples of randomised trials in interventional cardiology, including evaluation of both pharmacological and device treatments in acute coronary syndromes, myocardial infarction, elective percutaneous coronary intervention and structural heart disease. Exposure and outcome data, often rigorously collected in the cardiac catheterisation laboratory or coronary care unit, tend to be of high quality and are often quantitative or adjudicated. The use of centralised core laboratories (e.g., angiographic, echocardiographic and electrocardiographic) and endpoint adjudication allows for standardised analysis and interpretation of the data. In addition to the assessment of drugs or devices, randomised trials in interventional cardiology have been performed to compare strategies of care, for example early invasive versus conservative management in the management of acute coronary syndrome.

To achieve a valid comparison between 2 or more treatment groups requires that the two groups be alike as much as possible with the only difference, on average, being the specific therapies under investigation. The best way to achieve this balance is by the process of randomisation – each subject has an equal chance of assignment to intervention or control. It eliminates conscious bias (due to physician or patient preference; known confounders) as well as unconscious bias due to unknown factors (unknown confounders), resulting in treatment groups that are “alike on average”. Thus, in a well-developed and conducted RCT, we expect that all patient covariates, measured and unmeasured, are balanced between the two groups. Confounding is not a threat to the internal validity of a properly conducted RCT, and the observed treatment difference is an unbiased estimate of the true treatment difference.

Common randomisation techniques include simple randomisation, block randomisation, and stratified randomisation. Simple randomisation is based on a single sequence of random assignments (e.g., coin toss or computer-generated random numbers), and is simple and easy to implement. Although simple randomisation will likely generate similar numbers of participants among groups in large trials (n > 200), this is not guaranteed. In small trials there may be substantial differences in group sizes. One method to prevent unequal treatment group sizes is block randomisation. Block sizes are typically a multiple of the number of groups (i.e., with 2 treatment groups, block size of either 4 or 6). Once a block size has been determined, all possible balanced combinations of assignment within the block are calculated. Blocks are then randomly chosen to determine the participants’ assignment into the groups. While block randomisation prevents unequal group sizes, differences may occur in the distribution of baseline characteristics (covariates) in the groups (e.g., age distribution, diabetes). Stratified randomisation is commonly used to guard against a possible imbalance in baseline covariates. Specific covariates of interest are identified during trial design and a separate block is created for each combination of covariates. Participants are then stratified into risk subgroups (or strata) according to their baseline characteristics and then assigned to the appropriate block of covariates. Once all participants have been assigned into blocks, randomisation is performed within each block to assign participants to one of the treatment groups. The final result is a forced balance of treatment groups according to the covariates used to form the strata.

While the advantages of randomisation seem obvious, there are potential disadvantages or limitations. Although randomisation aims to ensure that the two groups are alike, it does not guarantee that the two treatment groups will be balanced. In addition, one has to ensure that equipoise genuinely exists for a RCT to be considered. Even when equipoise exists, timely recruitment of patients is important, particularly in the evaluation of new devices or concomitant medical therapy that can evolve rapidly. To enroll sufficient patients within a limited time-frame in large randomised trials, patients are often recruited at multiple locations. Such multicentre trials, in addition, may lead to greater generalizability than single-centre trials.

Randomised trials also usually employ strict enrolment criteria (both inclusion and exclusion) that are used to increase the internal validity of the study. This inherently limits the extent to which the results can be generalised to the general population seen in clinical practice (the “external validity”). In fact, there is often an inverse relationship between internal and external validity. This selective recruitment of patients in randomised trials on the basis of age, gender or comorbidities may result in differences in the efficacy or effectiveness of a therapy seen in RCTs compared with real-world settings. For example, elderly patients or patients with renal impairment are often excluded from randomised trials.

Randomised controlled trials are also generally designed to answer a narrow question or have a narrow focus that makes it difficult to anticipate rare but important adverse events or complications of a therapy. This difficulty is especially important when the complication may already be “common” in the population (e.g., myocardial infarction), if adverse events are delayed or do not manifest for several years, or if a potential exists for interactions with other comorbidities or medications in the community.

The Consolidated Standards of Reporting Trials (CONSORT) statement was developed to provide evidence-based recommendations for reporting of RCTs [33. Begg C, Cho M, Eastwood S, Horton R, Moher D, Olkin I, Pitkin R, Rennie D, Schulz KF, Simel D, Stroup DF. Improving the quality of reporting of randomized controlled trials. The consort statement. JAMA. 1996;276:637-9. , 44. Moher D, Schulz KF, Altman DG. The CONSORT statement: revised recommendations for improving the quality of reports of parallel-group randomised trials. Lancet. 2001;357:1191-4.
The CONSORT statement provides guidance for the design and reporting of an RCT by use of a checklist and flow diagram depicting information from four stages of a trial (enrolment, intervention allocation, follow-up and analysis). It also enables readers to understand the design, conduct, analysis, and interpretation of an RCT in order to judge its reliability or the relevance of the findings]. The CONSORT statement consists of a checklist and a flow diagram for reporting of a RCT and offers a standard way for authors to prepare reports of trial findings in a clear and transparent manner. The checklist items focus on reporting how the trial was designed, analysed and interpreted, while the flow diagram displays the progress of all participants through the trial, from their enrolment to analysis, with particular emphasis on follow-up and any excluded cases ( Figure 1 ).

Illustrative examples

The first drug-eluting stent (DES), the sirolimus-eluting stent (SES; Cypher®; Cordis Corporation, Johnson & Johnson, Warren, NJ, USA) was initially evaluated in the RAVEL trial (RAndomised study with the Sirolimus coated BX™ VElocity balloon expandable stent in the treatment of patients with De Novo native coronary artery Lesions) [55. Morice MC, Serruys PW, Sousa JE, Fajadet J, Ban Hayashi E, Perin M, Colombo A, Schuler G, Barragan P, Guagliumi G, Molnar F, Falotico R. A randomized comparison of a sirolimus-eluting stent with a standard stent for coronary revascularization. N Engl J Med. 2002;346:1773-80. ]. Briefly, this trial randomly assigned 238 patients with relatively low-risk lesions to treatment with the SES or bare metal stent (BMS) controls. The primary endpoint was a surrogate endpoint (discussed later in the chapter), namely in-stent late luminal loss (the difference between the minimal luminal diameter immediately after the procedure and the diameter at six months). At six months, the mean late luminal loss was significantly lower in the SES group than in the BMS. At 1-year follow-up, the rate of binary stenosis was 0.0% and 26.6% for patients treated with SES and BMS, respectively (p<0.001) [55. Morice MC, Serruys PW, Sousa JE, Fajadet J, Ban Hayashi E, Perin M, Colombo A, Schuler G, Barragan P, Guagliumi G, Molnar F, Falotico R. A randomized comparison of a sirolimus-eluting stent with a standard stent for coronary revascularization. N Engl J Med. 2002;346:1773-80. ].

The clinical benefits of DES were subsequently confirmed in the much larger randomised, double blind SIRIUS (Sirolimus-Eluting Stent in De-Novo Native Coronary Lesions) trial [66. Moses JW, Leon MB, Popma JJ, Fitzgerald PJ, Holmes DR, O’Shaughnessy C, Caputo RP, Kereiakes DJ, Williams DO, Teirstein PS, Jaeger JL, Kuntz RE. Sirolimus-eluting stents versus standard stents in patients with stenosis in a native coronary artery. N Engl J Med. 2003;349:1315-23. ] that enrolled 1,058 patients in 53 centres with relatively more complex lesions and patients than were seen in the RAVEL study. Nevertheless, the trial population was restricted to patients with stable or unstable angina and disease in native coronary artery measuring 15 mm to 30 mm in length; patients with recent myocardial infarction, an ejection fraction of less than 25%, or more complex lesion subsets such as bifurcation were excluded from the study. Unlike the RAVEL trial, the primary endpoint was a clinical composite endpoint failure of the target vessel (a composite of death from cardiac causes, myocardial infarction, and repeated percutaneous or surgical revascularisation of the target vessel) within 270 days. The rate of target vessel failure was reduced from 21.0% with a BMS to 8.6% with a SES (p<0.001) [66. Moses JW, Leon MB, Popma JJ, Fitzgerald PJ, Holmes DR, O’Shaughnessy C, Caputo RP, Kereiakes DJ, Williams DO, Teirstein PS, Jaeger JL, Kuntz RE. Sirolimus-eluting stents versus standard stents in patients with stenosis in a native coronary artery. N Engl J Med. 2003;349:1315-23. ].

This and other initial randomised studies ultimately led to regulatory approval for DES and their widespread use in clinical practice. These early generation sirolimus and paclitaxel eluting DES were superseded by the introduction of second generation DES with thinner stent struts, more biocompatible and durable polymer coatings and new limus based antiproliferative drugs – Xience (Abbott Vascular, California, USA) and Promus (Boston Scientific, Massachusetts, USA) everolimus eluting stents (EES) as well as Resolute (Medtronic, California, USA) zotarolimus eluting stents [77. Stone GW, Rizvi A, Newman W, Mastali K, Wang JC, Caputo R, Doostzadeh J, Cao S, Simonton CA, Sudhir K, Lansky AJ, Cutlip DE, Kereiakes DJ. Everolimus-Eluting versus Paclitaxel-Eluting Stents in Coronary Artery Disease. N Engl J Med. 2010;362:1663–1674. , 88. Yeh RW, Silber S, Chen L, Chen S, Hiremath S, Neumann F-J, Qiao S, Saito S, Xu B, Yang Y, Mauri L. 5-Year Safety and Efficacy of Resolute Zotarolimus-Eluting Stent: The RESOLUTE Global Clinical Trial Program. JACC Cardiovasc Interv. 2017;10:247–254. ].

Stent technology continues to improve and novel DES with biodegreable polymer coatings, polymer free DES as well as fully bioabsorbale coronary scaffolds have been developed and are currently under clinical investigation. Furthermore, whereas studies performed after approval have examined more extended uses of DES, there is a trend to begin DES evaluation with more broadly inclusive trials. The Synergy stent (Boston Scientific, Massachusetts, USA) is a platinum-chromium metal alloy platform with an ultrathin bioabsorbable abluminal everolimus-eluting polymer and it was compared with the Promus Element EES in the randomised EVOLVE I, and the larger EVOLVE II clinical trial [99. Kereiakes DJ, Meredith IT, Windecker S, Jobe RL, Mehta SR, Sarembock IJ, Feldman RL, Stein B, Dubois C, Grady T, Saito S, Kimura T, Christen T, Allocco DJ, Dawkins KD. Efficacy and Safety of a Novel Bioabsorbable Polymer-Coated, Everolimus-Eluting Coronary Stent (EVOLVE II). Circ Cardiovasc Interv. 2015;8. ]. In the latter trial of 1684 patients with NSTEMI or stable CAD undergoing PCI, the Synergy stent was noninferior to the Promus stent with respect to one year target lesion failure. While specific high risk patient (e.g. STEMI) and lesion subsets (e.g. vein grafts, left main) were excluded from the study, the study population reflected more contemporary clinical PCI practice compared with earlier generation DES trials for regulatory approval. The LEADERS (Limus Eluted from A Durable versus ERodable Stent coating) study is another example of this trend in more inclusive clincial trials [1010. Windecker S, Serruys PW, Wandel S, Buszman P, Trznadel S, Linke A, Lenk K, Ischinger T, Klauss V, Eberli F, Corti R, Wijns W, Morice MC, di Mario C, Davies S, van Geuns RJ, Eerdmans P, van Es GA, Meier B, Juni P. Biolimus-eluting stent with biodegradable polymer versus sirolimus-eluting stent with durable polymer for coronary revascularisation (Leaders): A randomised non-inferiority trial. Lancet. 2008;372:1163-73. ]. This was a large randomised trial comparing a Biolimus A9-eluting stent to SES with a durable polymer, where the main exclusion criteria were limited to 1) lesion parameters not suitable for the available stent size, or 2) inability to comply with dual antiplatelet therapy.

The Dual Antiplatelet Therapy (DAPT) trial was a large multicenter, randomized, placebo controlled trial to assess the benefits and risks of contnuing DAPT beyond 1 year after placement of DES in patients with stable CAD or ACS [1111. Mauri L, Kereiakes DJ, Yeh RW, Driscoll-Shempp P, Cutlip DE, Steg PG, Normand S-LT, Braunwald E, Wiviott SD, Cohen DJ, Holmes DR, Krucoff MW, Hermiller J, Dauerman HL, Simon DI, Kandzari DE, Garratt KN, Lee DP, Pow TK, Ver Lee P, Rinaldi MJ, Massaro JM. Twelve or 30 Months of Dual Antiplatelet Therapy after Drug-Eluting Stents. N Engl J Med. 2014;371:2155–2166. ]. While enrolling a broad range patients reflecting contemporary clinical practice, the study was powered to reliably ascertain rare clinical endpoints such as stent thrombosis, which was a coprimary efficacy endpoint along with major adverse cardiovascular and cerebrovascular events (a composite of death, myocardial infarction, or stroke). The trial showed that DAPT beyond 1 year after PCI with DES, as compared with aspirin therapy alone, significantly reduced the risks of stent throm- bosis (0.4% vs. 1.4%; HR, 0.29, 95% CI, 0.17 to 0.48; P<0.001) and major adverse cardiovascular and cerebrovascular events but was associated with an increased risk of bleeding.

Interestingly, the process of performing a randomised trial is in itself a selection process, because of the need to obtain informed consent, so that the trial population is not the same as that treated in the completely inclusive general practice. While these studies have the advantage of being representative of a broader population than the original narrowly designed studies, some caution is required. Unlike randomised trials that may be specifically designed and powered to examine a subgroup, such as acute myocardial infarction [1212. Stone GW, Lansky AJ, Pocock SJ, Gersh BJ, Dangas G, Wong SC, Witzenbichler B, Guagliumi G, Peruga JZ, Brodie BR, Dudek D, Mockel M, Ochala A, Kellock A, Parise H, Mehran R. Paclitaxel-eluting stents versus bare-metal stents in acute myocardial infarction. N Engl J Med. 2009;360:1946-59. ], multivessel or left main stent treatment [1313. Serruys PW, Morice MC, Kappetein AP, Colombo A, Holmes DR, Mack MJ, Stahle E, Feldman TE, van den Brand M, Bass EJ, Van Dyck N, Leadley K, Dawkins KD, Mohr FW. Percutaneous coronary intervention versus coronary-artery bypass grafting for severe coronary artery disease. N Engl J Med. 2009;360:961-72. ], these broad studies that are generally not designed and powered for subgroups suffer the same limitations of multiple testing when inferences are made on subgroups, particularly when treatment effect heterogeneity is plausible. Nonetheless, they possess the advantage of rapid recruitment, because of less restrictive screening, and the ability to examine a broader population at an earlier time in the DES evaluation process. Even then, certain subgroups (e.g., ST-elevation myocardial infarction (STEMI), left main, vein grafts for DES trials) might still be under-represented in all-comer trials and may need specific studies.

Superiority vs. non-inferiority trials

Broadly speaking, there are two types of randomised trial, superiority and non-inferiority trials. Superiority trials are by far the most frequent trials and aim to determine if sufficient evidence exists to show that one therapy is different from and superior to the other. This is the case when a new therapy is compared to placebo control or where a new therapy is expected to be better than an existing therapy.

In the absence of effective therapy, placebo-controlled trials are not contentious. However, when an effective therapy exists, performing a placebo-controlled trial would be unethical. A new experimental therapy might not be more efficacious than existing proven therapy but may offer other advantages such as safety (less invasive, less toxic), tolerability, convenience of administration or cost savings. Such a therapy might be tested against the standard therapy (an active control arm) in a non-inferiority trial.

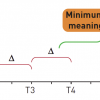
The objective of a non-inferiority clinical trial is to establish that the effect of the new treatment is statistically and clinically not inferior to the active control by a pre-stated non-inferiority margin. This non-inferiority margin (or “delta”) must be pre-specified and is based on clinical judgment and statistical reasoning. The margin is how much the control arm efficacy can exceed the new experimental treatment arm efficacy such that the experimental treatment can still be considered to be non-inferior to the control therapy. A positive non-inferiority trial implies that the experimental therapy is better than or no worse than the control therapy by at least the value of delta. In other words, the margin is the maximum clinically acceptable difference in efficacy between the new and existing therapy that one is willing to give up. An appropriate, a priori determination of an acceptable but conservative (not too liberal/wide or too restrictive/stringent) non-inferiority margin is paramount [1414. D’Agostino RB Sr, Massaro JM, Sullivan LM. Non-inferiority trials: design concepts and issues - the encounters of academic consultants in statistics. Stat Med. 2003;22:169-86. This paper provides an excellent review of the principles and issues involved with the design of non-inferiority trials.
It discusses guidelines for the selection of an active control, possible methods for selection of the non-inferiority margin and the assumptions underlying a non-inferiority trial]. Ideally, the margin should be smaller than the lower 95% confidence limit for the absolute treatment difference observed between existing standard therapy and placebo (the “95%-95% confidence interval method”) [1515. Kaul S, Diamond GA. Good enough: A primer on the analysis and interpretation of noninferiority trials. Ann Intern Med. 2006;145:62-69. , 1616. Rothmann M, Li N, Chen G, Chi GY, Temple R, Tsou HH. Design and analysis of non-inferiority mortality trials in oncology. Stat Med. 2003;22:239-64. ]. Non-inferiority is then inferred if the upper limit of the confidence interval (CI) for the difference between the new and the standard treatment is smaller than the margin. A more widely used strategy, however, is to define the margin as preserving a fraction (commonly 50%) of the established active control effect versus placebo [1414. D’Agostino RB Sr, Massaro JM, Sullivan LM. Non-inferiority trials: design concepts and issues - the encounters of academic consultants in statistics. Stat Med. 2003;22:169-86. This paper provides an excellent review of the principles and issues involved with the design of non-inferiority trials.
It discusses guidelines for the selection of an active control, possible methods for selection of the non-inferiority margin and the assumptions underlying a non-inferiority trial]. In other words, the new treatment retains at least 50% of the superiority of the existing active control over placebo.

The choice of the non-inferiority margin has a significant impact on the determination of the trial sample size. Compared to placebo-controlled trials, non-inferiority trials typically have larger sample sizes because the margin is much smaller than the treatment difference for which the placebo-controlled trial is powered.

It is important that the active-control comparator chosen in a non-inferiority trial is the best available standard of care. Otherwise, a phenomenon known as bio- or placebo-creep may occur when a slightly inferior therapy becomes the active control for the next generation of non-inferiority trials and so on until the newer active controls no longer become or remain superior to placebo ( Figure 2 ) [1414. D’Agostino RB Sr, Massaro JM, Sullivan LM. Non-inferiority trials: design concepts and issues - the encounters of academic consultants in statistics. Stat Med. 2003;22:169-86. This paper provides an excellent review of the principles and issues involved with the design of non-inferiority trials.
It discusses guidelines for the selection of an active control, possible methods for selection of the non-inferiority margin and the assumptions underlying a non-inferiority trial].

In general, superiority trials provide stronger evidence and offer greater credibility than non-inferiority trials with active controls. The analysis and interpretation of non-inferiority trials is based on a number of assumptions that may be difficult to justify or verify, such as the appropriate determination of a suitable non-inferiority margin, the consideration of prior placebo-controlled trials to establish superiority of the existing therapy (assay sensitivity) and the assumption that the historical difference between active control and placebo holds in the setting of the new trial if a placebo had been used (constancy assumption) [1414. D’Agostino RB Sr, Massaro JM, Sullivan LM. Non-inferiority trials: design concepts and issues - the encounters of academic consultants in statistics. Stat Med. 2003;22:169-86. This paper provides an excellent review of the principles and issues involved with the design of non-inferiority trials.
It discusses guidelines for the selection of an active control, possible methods for selection of the non-inferiority margin and the assumptions underlying a non-inferiority trial].

Interpretation of non-inferiority trials is based on where the confidence intervals (CI) for the treatment difference lies relative to the non-inferiority margin (delta) and the null effect. Non-inferiority trials may base their interpretation on the upper limit of a 1-sided 97.5% confidence interval, which is the same as the upper limit of a 2-sided 95% confidence interval. Possible trial outcome scenario CIs are shown in Figure 3. Once non-inferiority is shown, it may be acceptable then to assess whether the new treatment is superior to the reference treatment using appropriate a priori defined tests or confidence intervals. In such a case, the one-sided upper confidence boundary lies to the right of both the margin and the zero line of null effect ( Figure 2 ).

Because the design, analysis and interpretation of non-inferiority trials pose a particular challenge to investigators, clinicians and regulatory authorities, the Consolidated Standards of Reporting Trials (CONSORT) guidelines were recently expanded to address such trials [1717. Piaggio G, Elbourne DR, Altman DG, Pocock SJ, Evans SJ; CONSORT Group. Reporting of noninferiority and equivalence randomized trials: An extension of the CONSORT statement. JAMA. 2006;295:1152-60.
This extension of the Consolidated Standards of Reporting Trials Statement provides guidelines for the investigators and readers for the design, conduct, analysis and interpretation of non-inferiority and equivalence trials along with illustrative examples].

Illustrative example

The Acute Catheterization and Urgent Intervention Triage Strategy (ACUITY) trial is representative of a typical non-inferiority trial [1818. Stone GW, McLaurin BT, Cox DA, Bertrand ME, Lincoff AM, Moses JW, White HD, Pocock SJ, Ware JH, Feit F, Colombo A, Aylward PE, Cequier AR, Darius H, Desmet W, Ebrahimi R, Hamon M, Rasmussen LH, Rupprecht HJ, Hoekstra J, Mehran R, Ohman EM. Bivalirudin for patients with acute coronary syndromes. N Engl J Med. 2006;355:2203-16. ]. This was a prospective, open-label, randomised, multicentre trial in which bivalirudin alone (investigational treatment) was compared with bivalirudin plus a glycoprotein IIb/IIIa inhibitor (another investigational treatment strategy) and heparin plus a glycoprotein IIb/IIIa inhibitor (standard therapy) in 13,819 patients with moderate-risk or high-risk acute coronary syndromes who were undergoing an early invasive strategy. A placebo-controlled trial of the new treatment, bivalirudin, could not be justified, as withholding existing proven therapy with platelet glycoprotein IIb/IIIa inhibitor and an antithrombotic agent (unfractionated heparin) would be considered unethical in these patients.

In designing the trial the investigators decided on a relative margin of 25% (1.25 risk ratio) with non-inferiority being declared if the upper limit of the one-sided 97.5% confidence interval (CI) for the event rate in the investigational group did not exceed a relative margin of 25% from the event rate in the control group (equivalent to a 1-sided test with an alpha value of 0.025). They performed a sequential non-inferiority and superiority analyses and a 2-sided alpha value of 0.05 was used for superiority testing. The trial was powered for separate comparisons between the control group and each of the two investigational groups. Based on the non-inferiority margin and the anticipated 30-day event rates for the 3 primary endpoints [ a) composite ischaemia (death, myocardial infarction, or unplanned revascularisation for ischaemia), b) major bleeding, and c) net clinical outcome (combination of composite ischaemia or major bleeding)] of 6.5%, 9.0% and 12.4% in the control group, the investigators determined that a sample size of 4,600 patients per group was required to demonstrate non-inferiority for the comparison of bivalirudin alone with heparin plus glycoprotein IIb/IIIa inhibitors with 87%, 99% and 99% power for each of the 3 primary endpoints, respectively. Bivalirudin alone, as compared with heparin plus a glycoprotein IIb/IIIa inhibitor, was associated with a non-inferior rate of the composite ischaemia endpoint (7.8% and 7.3%, respectively; p=0.32; relative risk, 1.08; 95% confidence interval [CI], 0.93 to 1.24) and significantly reduced rates of major bleeding (3.0% vs. 5.7%; p<0.001; relative risk, 0.53; 95% CI, 0.43 to 0.65) and the net clinical outcome endpoint (10.1% vs. 11.7%; p=0.02; relative risk, 0.86; 95% CI, 0.77 to 0.97) [1818. Stone GW, McLaurin BT, Cox DA, Bertrand ME, Lincoff AM, Moses JW, White HD, Pocock SJ, Ware JH, Feit F, Colombo A, Aylward PE, Cequier AR, Darius H, Desmet W, Ebrahimi R, Hamon M, Rasmussen LH, Rupprecht HJ, Hoekstra J, Mehran R, Ohman EM. Bivalirudin for patients with acute coronary syndromes. N Engl J Med. 2006;355:2203-16. ].

This large trial also highlights some of the difficulties with the design and interpretation of non-inferiority trials. Choosing an appropriate non-inferiority margin is challenging and some have argued that a margin of 25% used in the study was perhaps too wide, with insufficient statistical or clinical justification and larger than other recent trials in ACS [1919. Kaul S, Diamond GA. Making sense of noninferiority: A clinical and statistical perspective on its application to cardiovascular clinical trials. Prog Cardiovasc Dis. 2007;49:284-99. ]. Also, interpretation of the results of a composite endpoint that combines both safety and efficacy measures may occasionally be difficult in a non-inferiority setting, as investigational treatments that are relatively ineffective but safer may be made to look as good as or better than effective treatments, biasing the assessment of non-inferiority in favour of the investigational treatment [1919. Kaul S, Diamond GA. Making sense of noninferiority: A clinical and statistical perspective on its application to cardiovascular clinical trials. Prog Cardiovasc Dis. 2007;49:284-99. ].

The Evaluation of XIENCE versus Coronary Artery Bypass Surgery for Effectiveness of Left Main Revascularization (EXCEL) trial was an open label multicentre trial that compared PCI with everolimus-eluting stents with CABG in patients with left main coronary disease [2020. Stone GW, Sabik JF, Serruys PW, Simonton CA, Généreux P, Puskas J, Kandzari DE, Morice M-C, Lembo N, Brown WM, Taggart DP, Banning A, Merkely B, Horkay F, Boonstra PW, van Boven AJ, Ungi I, Bogáts G, Mansour S, Noiseux N, Sabaté M, Pomar J, Hickey M, Gershlick A, Buszman P, Bochenek A, Schampaert E, Pagé P, Dressler O, Kosmidou I, Mehran R, Pocock SJ, Kappetein AP. Everolimus-Eluting Stents or Bypass Surgery for Left Main Coronary Artery Disease (EXCEL). N Engl J Med. 2016;375:2223-35. ]. The primary endpoint was a composite of the rate of all cause death, stroke and myocardial infarction at 3 years. The trial randomly assigned 1905 eligible patients with left main disease and was powered for non-inferiority testing of the primary endpoint. Although the assumed expected primary endpoint event rate at a median of 3 years was 11% in both treatment groups, a non-inferiority margin of 4.2% for the primary endpoint was chosen for the study after discussion with multiple stakeholders including interventional cardiologists and cardiac surgeons, and considered appropriate given the expected lower periprocedural morbidity of PCI compared with CABG. At a median follow-up of 3 years, the primary endpoint occurred in 15.4% of the patients in the PCI arm versus 14.7% in the CABG arm (difference 0.7%; upper 97.5% confidence limit, 4.0%). The trial met the criteria for non-inferiority as the upper 97.5% CI limit of the difference in the 3 year incidence rate of the primary endpoint, 4%, was less than the non-inferiority margin of 4.2%. In other words, PCI was non-inferior to CABG with respect to the rate of composite of death, stroke or myocardial infarction. However, PCI was not superior to CABG as the upper 97.5% CI limit was not less than zero.

The Nordic-Baltic-British left main revascularisation study (NOBLE) was another prospective, randomised, open-label, non-inferiority trial that assessed revascularization with PCI (most with Biolimus-eluting stent; 11% had 1^st generation DES) versus CABG in unprotected left main coronary artery stenosis in 1201 patients [2121. Mäkikallio T, Holm NR, Lindsay M, Spence MS, Erglis A, Menown IBA, Trovik T, Eskola M, Romppanen H, Kellerth T, Ravkilde J, Jensen LO, Kalinauskas G, Linder RBA, Pentikainen M, Hervold A, Banning A, Zaman A, Cotton J, Eriksen E, Margus S, Sørensen HT, Nielsen PH, Niemelä M, Kervinen K, Lassen JF, Maeng M, Oldroyd K, Berg G, Walsh SJ, Hanratty CG, Kumsars I, Stradins P, Steigen TK, Fröbert O, Graham ANJ, Endresen PC, Corbascio M, Kajander O, Trivedi U, Hartikainen J, Anttila V, Hildick-Smith D, Thuesen L, Christiansen EH, NOBLE study investigators. Percutaneous coronary angioplasty versus coronary artery bypass grafting in treatment of unprotected left main stenosis (NOBLE): a prospective, randomised, open-label, non-inferiority trial. Lancet. 2016;6736:1–10. ]. The primary endpoint was major adverse cardiac or cerebrovascular events (MACCE), a composite of all-cause mortality, non-procedural myocardial infarction, any repeat coronary revascularisation, and stroke. In this trial, the non–inferiority margin was based on a 12–month MACCE rate of 12% in the CABG group and 16% in the PCI subgroup of the SYNTAX study, and defined as a hazard ratio of 1.35 for PCI versus CABG. Kaplan-Meier 5 year estimates of the primary outcome were 29% for PCI and 19% for CABG (hazard ratio 1.48, 95% CI 1.11–1.96). Thus, as the upper end of the 95% CI of the hazard ratio exceeded 1.35, the study did not meet its primary endpoint and PCI was found to be inferior to CABG for treatment of left main coronary stenosis.

These two recent trials of LM PCI have yielded conflicting results. These likely reflect differences in trial design and length of follow-up. In NOBLE trial the primary endpoint included repeat revascularization whereas the EXCEL trial did not. Also, periprocedural MI was included as part of the MI definition within the primary endpoint in EXCEL (higher in CABG group than PCI group) but not in NOBLE. Furthermore, the stroke rate was higher with PCI in NOBLE, an unexpected finding based on prior studies, and not seen in EXCEL at 3 years.

Common randomised controlled trial designs

The common designs for randomised trials are illustrated in Figure 4. In the absence of a current standard of care, the new treatment is evaluated compared to a placebo control. Where a standard treatment exists, the new therapy may be compared directly against the standard or one may compare the standard to combination therapy that involves the standard plus the new therapy.

A factorial trial design is one in which participants are allocated to receive no intervention, one or the other treatment, or both. Such trials may be used to make two or more different therapeutic comparisons in the same trial (allow simultaneous tests of two experimental treatments in the same population). Each treatment (e.g., treatment A) is given to half the patients randomised (as opposed to one quarter in a conventional parallel group design), thereby increasing the efficiency. It is possible in a factorial trial to test for both the separate effects of each intervention and the benefits of receiving both interventions together. However, one of the limitations with a factorial design is an assumption of no interaction between the two therapies being studied, that is, the effect of each intervention is not influenced by the presence or absence of the other, and to test for interaction would require a much larger sample size.

Unplanned cross-overs in a RCT introduce bias. However, in a prospective cross-over design, each patient is given a series of two or more treatments over separate equal periods of time. In principle, such within-patient trials allow a more precise comparison of treatments and, hence, need a much smaller sample size. Such trials are appropriate when one is concerned with short-term response measured during and immediately following the treatment. Long-term carry-over effects of the first treatment into the second period are, thus, undesirable for this type of study. To avoid this carry-over effect influencing the outcome, a washout period, where patients do not receive any treatment, may be incorporated into the design.

An example of a factorial trial design is the ongoing Apixaban versus Warfarin in Patients with AF and ACS or PCI (AUGUSTUS) trial [2222. AUGUSTUS Trial. ClinicalTrials.gov Identifier NCT02415400. Available from: https://clinicaltrials. gov/ct2/show/study/NCT02415400. ]. In this mulitcentre trial of 4600 participants with AF needing oral anticoagulation and presenting with either ACS and/or requiring PCI with stent with subsequent planned P2Y12 receptor inhibitor for the next 6 months, will be randomised in a 2 x 2 factorial design, comparing open label apixaban (5 mg bid) versus warfarin (INR 2-3) as well as blinded aspirin versus placebo. The primary outcome is major or clinically relevant bleeding at 6 months, and secondary outcomes include death, MI, stroke and stent thrombosis.

Blinding

In order to have a fair and unbiased evaluation of randomised treatments, the outcome measures should ideally be evaluated in a blinded manner, where both the patient and the investigator responsible for evaluation of outcome are unaware of the treatment assignment (“double blinded”). This is particularly important when the outcome measures or clinical endpoints are subjective in nature. Blinding requires the use of placebo control where no standard therapy exists for comparison. Placebos improve the comparability of the two treatment groups in terms of compliance and follow-up and allow for an objective appraisal of the side-effects of treatment. While “double blinding” is ideal, it is not always feasible to perform a clinical trial in a blinded fashion (e.g., studies involving different types of intervention such as percutaneous vs. surgical) or it may only be feasible to blind the patient but not the treating physician to the treatment assignment (“single blinded”).

The importance of blinding was demonstrated in the recent trials of catheter based renal denervation in treatment-resistant hypertension. The first randomized trial, SIMPLICTY HTN-2, was an open label study that showed at 6 months, significant reductions in office based blood pressure in the treatment group compared with control (mean difference 33/11 mmHg, P <0.0001) [2323. Symplicity HTN-2 Investigators, Esler MD, Krum H, Sobotka PA, Schlaich MP, Schmieder RE, Böhm M. Renal sympathetic denervation in patients with treatment-resistant hypertension (The Symplicity HTN-2 Trial): a randomised controlled trial. Lancet. 2010;376:1903–9. ]. However, in the subsequent larger, single-blind, sham-controlled randomized trial, SYMPLICITY HTN-3, renal denervation was found to be ineffective for reduction in office systolic blood pressure at 6 months [2424. Bhatt DL, Kandzari DE, O’Neill WW, D’Agostino R, Flack JM, Katzen BT, Leon MB, Liu M, Mauri L, Negoita M, Cohen SA, Oparil S, Rocha-Singh K, Townsend RR, Bakris GL, SYMPLICITY HTN-3 Investigators. A controlled trial of renal denervation for resistant hypertension. SIMPLICITY HTN-3. N Engl J Med. 2014;370:1393–401. ]. The absence of blinding in the earlier randomized trial may have may have magnified the treatment effect.

Pragmatic Trials

Concerns that many trials are performed with relatively small samples at sites with experienced investigators and highly selected participants, where the therapeutic effects of the intervention may be overestimated and harms underestimated, has led to the consideration and design of more so called pragmatic trials. Such trials aim to increase generalizability by showing real-world effectiveness of the investigational drug or device in a broad range of patient population, with a view to informing clinical or policy decision.

The level of pragmatism in a clinical trial may be assessed with respect to (a) recruitment of investigators and participants – to what extent are the participants in the trial similar to patients who would potentially receive this intervention in usual care; (b) the intervention and its delivery – how different is the delivery of the intervention compared with the real world setting; (c) follow-up – how different is the intensity of follow-up in the trial compared with usual care; (d) analysis of outcomes – to what extent are all the data included in the analysis and how relevant is the primary outcome to the participants [2525. Loudon K, Treweek S, Sullivan F, Donnan P, Thorpe KE, Zwarenstein M. The PRECIS-2 tool: designing trials that are fit for purpose. BMJ Br Med J. 2015;350:h2147–h2147. ].

An example of recent pragmatic trial is the Thrombus Aspiration in ST Elevation Myocardial Infarction in Scandinavia (TASTE) trial [2626. Lagerqvist B, Fröbert O, Olivecrona GK, Gudnason T, Maeng M, Alström P, Andersson J, Calais F, Carlsson J, Collste O, Götberg M, Hårdhammar P, Ioanes D, Kallryd A, Linder R, Lundin A, Odenstedt J, Omerovic E, Puskar V, Tödt T, Zelleroth E, Östlund O, James SK. Outcomes 1 Year after Thrombus Aspiration for Myocardial Infarction. N Engl J Med. 2014;371:1111–1120. , 2727. Fröbert O, Lagerqvist B, Olivecrona GK, Omerovic E, Gudnason T, Maeng M, Aasa M, Angerås O, Calais F, Danielewicz M, Erlinge D, Hellsten L, Jensen U, Johansson AC, Kåregren A, Nilsson J, Robertson L, Sandhall L, Sjögren I, Östlund O, Harnek J, James SK. Thrombus Aspiration during ST-Segment Elevation Myocardial Infarction. N Engl J Med 2013;369:1587–1597. ]. This was a trial of routine manual thrombus aspiration before PCI versus PCI alone involving 7244 participants. The participants underwent randomization within an existing national registry (the Swedish Coronary Angiography and Angioplasty Registry, SCAAR, which is itself part of the broader Swedish Web System for Enhancement and Development of Evidence-Based Care in Heart Disease Evaluated According to Recommended Therapies, SWEDEHEART, registry) and thus achieved high participation due to simple design. Furthermore, there were no trial specific follow-up visits and follow-up data and outcomes were extracted from the registry database and record linkage to national discharge registry. The trial did not show a benefit in the primary endpoint of all-cause mortality at 30 days with routine thrombus aspiration, nor did it show a reduction in the rate all-cause death or the composite of all-cause death, rehospitalisation for myocardial infarction, or stent thrombosis at 1 year.

Alternatives to randomisation

OBSERVATIONAL STUDIES

The objective of an observational study is to study causal effects. Non-randomised trials may be appropriate for early studies of new and untried therapies (Phase I) or uncontrolled early phase studies (Phase II) where the standard is relatively ineffective. These are also commonly performed in the setting where randomised trials cannot be done within the current climate of controversy (no “clinical equipoise”). Lastly, they are an important tool in determining the effectiveness and safety of a therapy in clinical practice by allowing for the inclusion of broader populations of patients. Well-conducted observational studies can provide physicians and patients with a more realistic assessment of the real-world outcomes of therapies, as compared with traditional but more restrictive RCTs.

NON-RANDOMISED, CONCURRENTLY CONTROLLED TRIALS

In non-randomised, concurrently controlled trials, subjects are allocated to either treatment arm based on factors such as physician judgment or subject preference and not through a formal randomisation process. There is no guarantee that the patient covariates, measured and unmeasured, are balanced between the two treatment groups and the two treatment groups may, therefore, not be comparable.

Indeed, such studies may experience more rapid enrolment because patients are enrolled based on physician and patient preference. However, the interpretability of the resulting data may be questioned due to underlying bias and confounding. Selection bias is the major concern regarding the interpretation of non-randomised studies. If the patient characteristics are not comparable between the two treatment arms, these factors, if associated with the disease process and the outcome, may confound the true relationship between the therapeutic intervention and the outcome being studied.

For causal inference to be drawn from an observational study, statistical techniques such as multivariable regression analysis, matching or stratification and propensity score methods, can attempt to correct for known and measured confounders. However, effects of potential unknown or unmeasured factors can still affect the results, and in a non-randomised clinical trial the effects of bias and confounding cannot be expected to be completely eradicated.

Illustrative example

Randomised trials designed to evaluate DES have been limited to a less complex patient population than those currently treated in the general population [66. Moses JW, Leon MB, Popma JJ, Fitzgerald PJ, Holmes DR, O’Shaughnessy C, Caputo RP, Kereiakes DJ, Williams DO, Teirstein PS, Jaeger JL, Kuntz RE. Sirolimus-eluting stents versus standard stents in patients with stenosis in a native coronary artery. N Engl J Med. 2003;349:1315-23. ]. In addition, they have had limited power to detect small differences in adverse events such as stent thrombosis and mortality between DES and BMS. Some earlier observational studies raised the concern that, beyond the first year of treatment, DES may be associated with higher rates of such adverse events [2828. Lagerqvist B, James SK, Stenestrand U, Lindback J, Nilsson T, Wallentin L. Long-term outcomes with drug-eluting stents versus bare-metal stents in Sweden. N Engl J Med. 2007;356:1009-19. ]. These studies, while larger and more inclusive, may have been limited by completeness of follow-up and control of selection bias.

Several population-based studies have examined DES and BMS outcomes [2828. Lagerqvist B, James SK, Stenestrand U, Lindback J, Nilsson T, Wallentin L. Long-term outcomes with drug-eluting stents versus bare-metal stents in Sweden. N Engl J Med. 2007;356:1009-19. , 2929. Mauri L, Normand SL. Studies of drug-eluting stents: to each his own?. Circulation. 2008;117:2047-50.
This editorial briefly discusses the strengths and limitations of randomised clinical trials and well-conducted observational studies with reference to recent studies of drug-eluting stents, 3030. Mauri L, Silbaugh TS, Wolf RE, Zelevinsky K, Lovett A, Zhou Z, Resnic FS, Normand SL. Long-term clinical outcomes after drug-eluting and bare-metal stenting in Massachusetts. Circulation. 2008;118:1817-27. , 3131. Tu JV, Bowen J, Chiu M, Ko DT, Austin PC, He Y, Hopkins R, Tarride JE, Blackhouse G, Lazzam C, Cohen EA, Goeree R. Effectiveness and safety of drug-eluting stents in Ontario. N Engl J Med. 2007;357:1393-402. , 3232. Abbott JD, Voss MR, Nakamura M, Cohen HA, Selzer F, Kip KE, Vlachos HA, Wilensky RL, Williams DO. Unrestricted use of drug-eluting stents compared with bare-metal stents in routine clinical practice: Findings from the National Heart, Lung, and Blood Institute Dynamic Registry. J Am Coll Cardiol. 2007;50:2029-36. , 3333. Marzocchi A, Saia F, Piovaccari G, Manari A, Aurier E, Benassi A, Cremonesi A, Percoco G, Varani E, Magnavacchi P, Guastaroba P, Grilli R, Maresta A. Long-term safety and efficacy of drug-eluting stents: Two-year results of the REAL (registro angioplastiche dell’emilia romagna) multicenter registry. Circulation. 2007;115:3181-8. ]. A more recent example of comparison of outcomes of stent thrombosis and adverse cardiovascular events following DES or BMS in patients receiving dual antiplatelet therapy comes from the prespecified secondary analysis of the DAPT trial, comparing 12 or 30 months of therapy with dual antiplatelet therapy after PCI [3434. Stent Thrombosis in Drug-Eluting or Bare-Metal Stents in Patients Receiving Dual Antiplatelet Therapy. JACC Cardiovasc Interv. 2015;8:1552–1562. ]. In this trial, the choice of stent type (DES or BMS) was not randomly allocated, although the study inclusion and exclusion criteria, expected treatment with at least 12m dual antiplatelet therapy, and randomization criteria were the same in both stent groups. Nonetheless, as patients were not randomised to stent type, differences between DES and BMS treated subjects on observed confounders were expected. Thus, propensity score matching (based on the log-odds of the probability that a patient received a DES, modelled as a function of the confounders identified) was used to select a group of patients who were essentially similar according to all measured baseline variables (“pseudo-randomisation”). A BMS-treated subject was matched to as many as 8 DES-treated subjects without repalcement based on 55 known confounders. Matching by propensity score yielded 8308 DES-treated patients matched to 1718 BMS-treated patients and the success of the matches was determined by examining weighted standardised differences in the observed confounders between the matched DES and BMS groups, with absolute differences of <10% considered evidence of balance. The study concluded that among the propensity-matched subjects, DES treated patients had a lower rate of stent thrombosis at 33 months compared with BMS treated patients (1.7% vs. 2.6%, weighted risk difference 1.1%, p=0.01) and a non-inferior rate of MACCE (11.4% vs. 13.2%, p < 0.001). While propensity score matching on multiple variables was used to overcome confounding related to measured covariates, matching on the propensity score cannot be expected to balance unmeasured confounders that are not related to the measured confounders. Thus, potential presence of unknown confounders remains a limitation of this type of non-randomized analysis.

UNCONTROLLED OR HISTORICAL CONTROLLED TRIALS

In an uncontrolled trial the new therapy is studied without any direct comparison with a similar group of patients on standard or alternative therapy. The outcomes may be indirectly compared to the outcomes reported in the literature for a similar group of patients (“literature controls”). Such a trial design may be reasonable if the diseased patients are homogenous and their outcomes predictable and ascertained with similar methods across studies, and are more commonly used in the setting of Phase I and II studies. However, such trials have a significant potential for bias.

One of the most common non-randomised controlled trial designs is a retrospective comparison of the outcomes of the current patients on the new therapy to a similar group of patients in the past who received another standard therapy (“historical controls”), usually at the same institution. The advantages of such an approach are that such trials can be conducted with fewer resources as fewer patients are required (as compared to a RCT). However, while the patients are likely to be more homogenous than using literature controls, it is unlikely that the 2 groups are well balanced due to bias (e.g., patient selection) and confounding factors (e.g., ancillary care may be different with time). Statistical methods to control for such bias are important, but the change in outcomes as a function of time may not be overcome if it is independent of measured confounders.

Compared with retrospective cohort studies, in prospective cohort studies the investigator has control over what exposures and outcomes are measured. Single arm studies in interventional cardiology are a special type of uncontrolled prospective cohort study designed to assess proof of concept. An example of a single arm, first-in-human trial is the RESOLUTE trial [3535. Meredith IT, Worthley S, Whitbourn R, Walters DL, McClean D, Horrigan M, Popma JJ, Cutlip DE, DePaoli A, Negoita M, Fitzgerald PJ. Clinical and angiographic results with the next-generation Resolute stent system: A prospective, multicenter, first-in-human trial. JACC Cardiovasc Interv. 2009;2:977-85. ] of a new zotarolimus-eluting stent (ZES) using a novel polymer coating. This was a prospective, non-randomised multicentre trial of the Resolute stent system to assess its early feasibility, medium- term efficacy and safety on the basis of acute procedural success rate, in-segment late lumen loss (a surrogate endpoint) and major adverse cardiac events (MACE), respectively. Pivotal studies of this stent were also performed to provide data regarding US approval – one randomised [3838. Serruys PW, Silber S, Garg S, van Geuns RJ, Richardt G, Buszman PE, Kelbaek H, van Boven AJ, Hofma SH, Linke A, Klauss V, Wijns W, Macaya C, Garot P, DiMario C, Manoharan G, Kornowski R, Ischinger T, Bartorelli A, Ronden J, Bressers M, Gobbens P, Negoita M, van Leeuwen F, Windecker S. Comparison of zotarolimus-eluting and everolimus-eluting coronary stents. N Engl J Med. 2010;363:136-46. ] and another non-randomised, but historically controlled [3636. Yeung AC, Leon MB, Jain A, Tolleson TR, Spriggs DJ, Mc Laurin BT, Popma JJ, Fitzgerald PJ, Cutlip DE, Massaro JM, Mauri L. Clinical evaluation of the Resolute zotarolimus-eluting coronary stent system in the treatment of de novo lesions in native coronary arteries the RESOLUTE US clinical trial. J Am Coll Cardiol. 2011;57:1778-83. Epub 2011 Apr 4. ]. In the Resolute US Trial, by utilising the same inclusion and exclusion criteria as used in prior studies of the Endeavor® ZES (Medtronic, Minneapolis, MN, USA), and employing propensity score adjustment to correct for any residual variation, it was possible to compare patient-level information between trials using a uniform study endpoint of target lesion failure. A single arm study was a reliable method for this trial due to the nature of only a single aspect of the stent changing in reference to the comparator (only the drug-eluting polymer differed substantially) and the requirement for uniform data collection, definition and adjudication [3636. Yeung AC, Leon MB, Jain A, Tolleson TR, Spriggs DJ, Mc Laurin BT, Popma JJ, Fitzgerald PJ, Cutlip DE, Massaro JM, Mauri L. Clinical evaluation of the Resolute zotarolimus-eluting coronary stent system in the treatment of de novo lesions in native coronary arteries the RESOLUTE US clinical trial. J Am Coll Cardiol. 2011;57:1778-83. Epub 2011 Apr 4. , 3737. Mauri L, Leon MB, Yeung AC, Negoita M, Keyes MJ, Massaro JM. Rationale and design of the clinical evaluation of the Resolute zotarolimus-eluting coronary stent system in the treatment of de novo lesions in native coronary arteries (the Resolute US clinical trial). American Heart Journal. 2011;161:807-14. ].

Endpoints

PRIMARY ENDPOINT

The primary endpoint is the main outcome measure used to evaluate the results of the study and to answer the research question of interest. It also forms the basis for determination of the power of the study or the sample size required. Generally, a clinical trial should have only one primary endpoint, defined prior to study initiation. Multiple primary endpoints in a study may suggest that the study lacks a clear objective, and primary endpoints defined after study initiation or once the data are collected may indicate that the results are biased. Regulatory authorities and journals insist on a single primary endpoint that is defined in advance of study initiation along with the statistical analysis plan.

The primary endpoint should be clinically relevant, biologically important, and amenable to unbiased assessment. The endpoint events should occur frequently enough for the study to have statistical power. The time-frame for assessment of the endpoint after the therapeutic intervention is important: enough time must elapse for the intervention to have an effect on the endpoint, but the endpoint ascertainment should not be too far out in the future as it may reflect “noise”.

The most common endpoint type is one in which the patient response is dichotomous or binary, that is, each patient’s outcome can be classified as either a “success” or “failure”. In this case, the outcome in the treated group can be compared to the control group by considering the difference in the event rates in the 2 groups (P1 – P2). In a superiority RCT that compares these 2 treatments, we test the null hypothesis that there is no difference between the 2 treatments (H0: P1 – P2 = 0) against the alternative hypothesis of a treatment difference (HA: P1 – P2 ≠ 0). The statistical significance of the observed treatment response difference is based on a test of significance of the null hypothesis assuming that the null hypothesis is true: that is, if the null hypothesis of no treatment difference is true, what are the chances of getting as large a difference in response rates as that which has been observed? The reported p-value is the probability of observing what we have observed or more extreme, if the null hypothesis is true. A p-value of 0.05 or less is generally accepted as being significant but some studies will specify a higher degree of certainty (e.g., p-value of 0.025).

The primary endpoint serves as the basis for determination of the number of patients needed in the trial. In order to calculate the sample size prior to study initiation, an idea of the likely difference in event rates between the 2 treatment groups (∆ = P1 - P2) is required. These reflect realistic expectations of outcome based on previous studies or what is biologically plausible and considered to be clinically significant. Two other quantities need to be specified in order to be able to calculate the sample size: the power of the study, 1-β, where β is the probability of concluding that the treatments are not different when in fact they are different (type II error; risk of a false negative result), and α, which is the probability of concluding that the 2 groups are different when in fact they are not different (type I error; risk of a false positive result). In general, the α level is set at 0.05 and the power of the study at 0.8 (80%) to 0.9 (90%). Importantly, for a given power and α value, as the treatment difference between 2 groups increases (larger ∆), the sample size required to show significance decreases, and vice versa. The sample size calculation should ideally also take into account the anticipated proportion of patients that might be lost to follow-up.

Apart from measurement of event rates, other major endpoint types include time to an event or failure (comparison based on the ratio of the hazard rates in the 2 groups, e.g., survival analysis) and, in the case of a continuous outcome variable, the mean or average value (comparison based on the difference in the means in the 2 groups).

COMPOSITE ENDPOINTS

The use of composite endpoints (CEP) is common in cardiovascular trials, with one study reporting that 37% of over 1,200 trials over a 7-year period used a CEP [3939. Lim E, Brown A, Helmy A, Mussa S, Altman DG. Composite outcomes in cardiovascular research: A survey of randomized trials. Ann Intern Med. 2008;149:612-7. ]. A CEP consists of 2 or more binary endpoints and may be the primary endpoint of a trial. Patients experiencing any of the events from the eligible set (the components) of endpoints are considered to have experienced the CEP of interest. For instance, in a clinical trial that includes the CEP “death, myocardial infarction or revascularisation”, patients experiencing any of these 3 individual endpoints during the follow-up are considered to have experienced the CEP. The main advantage of use of CEPs is the need for a smaller sample size for a given level of power as a result of the increased event (failure) rate, and thereby improving trial efficiency.

To avoid the problem of introducing bias from competing risks, it is important that the CEP consists of the events of interest (e.g., myocardial infarction, revascularisation) and “anything worse” such as death. Also, the individual component endpoints should be reported separately in the trial (as secondary endpoints) to determine if the components are concordant and whether the CEP result is dominated by one of its components. Ideally, all components should demonstrate evidence of significant benefit. For example, in the HOPE (Heart Outcomes Prevention Evaluation) trial [4040. Yusuf S, Sleight P, Pogue J, Bosch J, Davies R, Dagenais G. Effects of an angiotensin-converting-enzyme inhibitor, ramipril, on cardiovascular events in high-risk patients. The heart outcomes prevention evaluation study investigators. N Engl J Med. 2000;342:145-53. ] of ramipril versus placebo in nearly 9,300 patients at high risk for cardiac events, ramipril significantly reduced the composite primary endpoint of myocardial infarction, stroke, or death from cardiovascular causes and all individual components demonstrated evidence of significant benefit (primary endpoint, relative risk, 0.78; 95 per cent confidence interval, 0.70 to 0.86; p<0.001; death from cardiovascular causes, relative risk, 0.74; p<0.001), myocardial infarction, relative risk, 0.80; p<0.001), stroke, relative risk, 0.68; p<0.001).

While there are definite advantages of CEP in increasing trial efficiency, this is not without limitations. All components of a CEP are considered statistically equivalent in the analysis, irrespective of their clinical importance (e.g., failure due to hospitalisation for heart failure is considered equivalent to death in a CEP). The results of a trial based on CEP may be difficult to interpret or potentially misleading if an overall positive effect of therapy is driven by a less serious component endpoint [4141. Kaul S, Diamond GA. Trial and error. How to avoid commonly encountered limitations of published clinical trials. J Am Coll Cardiol. 2010;55:415-27. This review discusses some of the potential limitations and challenges in the interpretation of the results of randomised controlled clinical trials. Using examples from recent cardiovascular RCTs, it discusses issues of clinical vs.
statistical significance of treatment effects, composite endpoints and subgroup analyses]. For example, some cardiovascular trials combine “hard” but uncommon clinical endpoints such as death, disabling stroke or spontaneous myocardial infarction (MI) with “softer” but more common endpoints such as hospitalisation, revascularisation or periprocedural MI (defined on the basis of biomarkers). These softer endpoints may then drive the composite treatment effect. For example, the benefit of prasugrel over clopidogrel in patients with acute coronary syndromes in TRITON-TIMI 38 (Trial to Assess Improvement in Therapeutic Outcomes by Optimizing Platelet Inhibition with Prasugrel - Thrombolysis in Myocardial Infarction 38) [4242. Wiviott SD, Braunwald E, McCabe CH, Montalescot G, Ruzyllo W, Gottlieb S, Neumann FJ, Ardissino D, De Servi S, Murphy SA, Riesmeyer J, Weerakkody G, Gibson CM, Antman EM. Prasugrel versus clopidogrel in patients with acute coronary syndromes. N Engl J Med. 2007;357:2001-15. ] was driven by non-fatal MI, a significant proportion of which were periprocedural MI based on biomarker elevation [4141. Kaul S, Diamond GA. Trial and error. How to avoid commonly encountered limitations of published clinical trials. J Am Coll Cardiol. 2010;55:415-27. This review discusses some of the potential limitations and challenges in the interpretation of the results of randomised controlled clinical trials. Using examples from recent cardiovascular RCTs, it discusses issues of clinical vs.
statistical significance of treatment effects, composite endpoints and subgroup analyses].

Interpretability may be challenging or further compromised in the more extreme situation where the treatment effects on individual components are in opposite directions. For instance, in the ASSENT-3 PLUS clinical trial (Assessment of the Safety and Efficacy of a New Thrombolytic Regimen in Acute Myocardial Infarction) [4343. Wallentin L, Goldstein P, Armstrong PW, Granger CB, Adgey AA, Arntz HR, Bogaerts K, Danays T, Lindahl B, Makijarvi M, Verheugt F, Van de Werf F. Efficacy and safety of tenecteplase in combination with the low-molecular-weight heparin enoxaparin or unfractionated heparin in the prehospital setting: The assessment of the safety and efficacy of a new thrombolytic regimen (Assent)-3 plus randomized trial in acute myocardial infarction. Circulation. 2003;108:135-42. ] to assess the efficacy and safety of Tenecteplase in combination with the low-molecular-weight heparin enoxaparin or unfractionated heparin in the pre-hospital setting, the primary efficacy-plus-safety CEP included efficacy outcomes (30-day mortality, in-hospital reinfarction or in-hospital refractory ischaemia) and safety outcomes (in-hospital ICH, in-hospital major bleeding other than intracranial). Tenecteplase with enoxaparin showed benefit for some of the efficacy outcomes (in-hospital reinfarction and refractory ischaemia: 3.5% vs. 5.8%, p=0.03 and 4.4% vs. 6.5%, p=0.07, respectively) but more harm for the safety outcomes (intracranial haemorrhage and major bleeding: 2.2% vs. 0.97%, p=0.04 and 4% vs. 2.8%, p=0.17, respectively), and 30-day mortality was numerically higher (7.5% vs. 6.0%, p=0.23) [4343. Wallentin L, Goldstein P, Armstrong PW, Granger CB, Adgey AA, Arntz HR, Bogaerts K, Danays T, Lindahl B, Makijarvi M, Verheugt F, Van de Werf F. Efficacy and safety of tenecteplase in combination with the low-molecular-weight heparin enoxaparin or unfractionated heparin in the prehospital setting: The assessment of the safety and efficacy of a new thrombolytic regimen (Assent)-3 plus randomized trial in acute myocardial infarction. Circulation. 2003;108:135-42. ]. The reduction in in-hospital myocardial infarction and refractory ischaemia was cancelled by the effect on intracranial haemorrhage and major bleeding (18.3% vs. 20.3%; p=0.3). This raises concerns about evaluating the “net-clinical” benefit. If all the components of the CEP were of similar clinical importance, one could consider combining the events and calculating the net-clinical benefit. However, most would agree that intracranial haemorrhage is a more significant adverse event compared with refractory ischaemia, and the risk of intracranial bleeds would lead most patients to reject the treatment even if there was an apparent overall benefit due to a reduction in refractory ischaemia.

Arguably, major adverse cardiac events (MACE) are the most common CEP used in interventional cardiology research. However, there is currently no consensus definition of MACE across trials and there is significant heterogeneity in the individual outcomes used to define composite endpoints. Usually this endpoint includes measures of safety (death, stroke, MI) and effectiveness (restenosis, revascularisation) of therapy [4444. Kip KE, Hollabaugh K, Marroquin OC, Williams DO. The problem with composite end points in cardiovascular studies: The story of major adverse cardiac events and percutaneous coronary intervention. J Am Coll Cardiol. 2008;51:701-7. ]. There is a potential for misleading interpretation depending on the definition of MACE used. For example, in randomised trials of drug-eluting versus bare metal stent one could potentially erroneously conclude that DES were significantly better at reducing death, MI and revascularisation in totality, even though the significant effect on this combined endpoint was driven primarily by a reduction in revascularisation [66. Moses JW, Leon MB, Popma JJ, Fitzgerald PJ, Holmes DR, O’Shaughnessy C, Caputo RP, Kereiakes DJ, Williams DO, Teirstein PS, Jaeger JL, Kuntz RE. Sirolimus-eluting stents versus standard stents in patients with stenosis in a native coronary artery. N Engl J Med. 2003;349:1315-23. ].

SECONDARY ENDPOINT

There may be multiple secondary endpoints in a study. These endpoints may be important for interpretation or explanation of the main findings of the study. These are often considered exploratory analyses and need to be interpreted with caution. A major concern when there are multiple endpoints evaluated is the risk of a false-positive result finding, i.e., the likelihood of finding a statistically significant result by chance alone increases with the number of tests undertaken. Pre-specifying a limited number of secondary endpoints of clinical importance can reduce the risk of a false-positive finding, and specific statistical measures can be undertaken to adjust for the likelihood of false positives. One such approach is to use a Bonferroni adjustment, by modifying the p-value at which significance is declared (i.e., if there are 2 secondary endpoints then consider a significant p-value of 0.025 for each endpoint comparison rather than 0.05). However, this is a conservative method, particularly when the outcome endpoints are correlated with one another, and other techniques, such as sequential testing procedures, exist to make appropriate adjustment for multiple testing. In any case, as with the primary endpoint, it is important to specify the secondary endpoints to be evaluated in the trial prior to the collection of the data and any statistical analysis.

Subgroup analysis

Clinical trials generally collect detailed baseline data on each patient, and it is reasonable to attempt to gain the maximum information from them. Subgroup analyses are frequently performed to examine whether treatment differences appear consistent across all types of patients or vary according to subgroups. For example, in the TRITON-TIMI 38 trial [4242. Wiviott SD, Braunwald E, McCabe CH, Montalescot G, Ruzyllo W, Gottlieb S, Neumann FJ, Ardissino D, De Servi S, Murphy SA, Riesmeyer J, Weerakkody G, Gibson CM, Antman EM. Prasugrel versus clopidogrel in patients with acute coronary syndromes. N Engl J Med. 2007;357:2001-15. ], a post hoc exploratory analysis identified patients at higher risk of bleeding (age > 75 years, body weight < 60 kg, history of prior stroke/transient ischaemic attack) which potentially has important implications for clinical practice and regulatory approval and labelling.

While it is interesting and important to identify the subgroups of patients for which the new therapy is more (or less) effective, several problems may arise from such analyses. Examining multiple subgroups is a form of multiple testing resulting in the risk of false-positive findings. The potential for false-positive errors is quite common – the probability of a false-positive error is equal to 1 – (1-a)ⁿ, where a is the false-positive error for each subgroup (usually 0.05) and n is the number of independent subgroup analyses. In addition, subgroups are generally underpowered and false negatives are also quite common.

Therefore, pre-specification of subgroups and cautious interpretation of these findings is essential. Such analyses should be considered as hypothesis-generating with plausible findings evaluated in further clinical trials. To guard against “data dredging” or post hoc data exploration, it is important that a limited number of subgroup analyses be pre-specified with a clear statement of the rationale for choosing them (based on biological mechanisms or the results of prior studies). Most trials are only sufficiently powered to detect the primary endpoint difference between the two treatment groups and, therefore, statistical tests on subgroups are often underpowered and may only have only enough power to detect very large subgroup effects. Finally, the most appropriate statistical method for making inference from a subgroup analysis is the test for interaction. A significant test for interaction of a subgroup with treatment suggests different treatment effects according to subgroup. While testing for interaction is widely recommended, a review of 50 consecutive clinical-trial reports from four major medical journals suggested that, while two-thirds of the reports presented subgroup findings, only 43% reported appropriate statistical tests for interaction [4545. Assmann SF, Pocock SJ, Enos LE, Kasten LE. Subgroup analysis and other (mis)uses of baseline data in clinical trials. Lancet. 2000;355:1064-9. ].

One should always be cautious of interpreting a subgroup treatment effect in a trial with no overall treatment effect. The results of the SYNTAX (Synergy between Percutaneous Coronary Intervention with Taxus and Cardiac Surgery) trial in patients with 3-vessel or left main coronary artery (LMCA) disease, or both, showed that percutaneous coronary intervention (PCI) using the TAXUS® DES (Boston Scientific, Natick, MA, USA) as compared with CABG was associated with a higher rate of MACE or cerebrovascular events at 1 year (17.8% vs. 12.4% for CABG; p=0.002), driven in large part by an increased rate of revascularisation in the PCI group [1313. Serruys PW, Morice MC, Kappetein AP, Colombo A, Holmes DR, Mack MJ, Stahle E, Feldman TE, van den Brand M, Bass EJ, Van Dyck N, Leadley K, Dawkins KD, Mohr FW. Percutaneous coronary intervention versus coronary-artery bypass grafting for severe coronary artery disease. N Engl J Med. 2009;360:961-72. ]. A post hoc subgroup analysis showed a trend towards lower events with PCI in cases with LMCA disease (LMCA only, 7.1% vs. 8.5%, relative risk 0.88, CI 0.21-3.69; and LMCA plus single-vessel disease 7.5% vs. 13.2%, relative risk 0.59, CI 0.21-1.67), compared with CABG-treated patients. Interaction testing shows that there was overlap between the treatment effect in the LMCA only cohort (interaction p=0.51) or LMCA plus single-vessel disease cohort (interaction p=0.10) and the effect in the overall cohort. While sub-group analyses for LMCA patients with low or intermediate SYNTAX scores suggested benefit of DES over CABG, this needs to be interpreted with caution and considered hypothesis-generating only. Such hypothesis was then later tested in adequately powered randomized trials of PCI versus CABG, such as EXCEL and NOBLE [2020. Stone GW, Sabik JF, Serruys PW, Simonton CA, Généreux P, Puskas J, Kandzari DE, Morice M-C, Lembo N, Brown WM, Taggart DP, Banning A, Merkely B, Horkay F, Boonstra PW, van Boven AJ, Ungi I, Bogáts G, Mansour S, Noiseux N, Sabaté M, Pomar J, Hickey M, Gershlick A, Buszman P, Bochenek A, Schampaert E, Pagé P, Dressler O, Kosmidou I, Mehran R, Pocock SJ, Kappetein AP. Everolimus-Eluting Stents or Bypass Surgery for Left Main Coronary Artery Disease (EXCEL). N Engl J Med. 2016;375:2223-35. , 2121. Mäkikallio T, Holm NR, Lindsay M, Spence MS, Erglis A, Menown IBA, Trovik T, Eskola M, Romppanen H, Kellerth T, Ravkilde J, Jensen LO, Kalinauskas G, Linder RBA, Pentikainen M, Hervold A, Banning A, Zaman A, Cotton J, Eriksen E, Margus S, Sørensen HT, Nielsen PH, Niemelä M, Kervinen K, Lassen JF, Maeng M, Oldroyd K, Berg G, Walsh SJ, Hanratty CG, Kumsars I, Stradins P, Steigen TK, Fröbert O, Graham ANJ, Endresen PC, Corbascio M, Kajander O, Trivedi U, Hartikainen J, Anttila V, Hildick-Smith D, Thuesen L, Christiansen EH, NOBLE study investigators. Percutaneous coronary angioplasty versus coronary artery bypass grafting in treatment of unprotected left main stenosis (NOBLE): a prospective, randomised, open-label, non-inferiority trial. Lancet. 2016;6736:1–10. ].

Surrogate endpoints

A surrogate endpoint is a physical sign or laboratory measurement that is used as a substitute for a clinically meaningful endpoint. A surrogate must not only be a correlate of the true clinical outcome but also, ideally, fully capture the net effect of treatment on the clinical outcome. Endpoints such as blood pressure, haemoglobin A1c and cholesterol levels have long been used in cardiovascular trials as surrogates for vascular events, including death, myocardial infarction and stroke. Their common use in cardiovascular clinical trials stems from several advantages. Commonly, surrogate endpoints are continuous endpoints that allow ascertainment of treatment differences at a smaller sample size. Surrogates may be easier to measure than “true” endpoints. They may be measured at an earlier time point compared with the final clinical endpoint. In interventional cardiology, angiographic measures such as late loss and per cent diameter stenosis are commonly used surrogates in the evaluation of the efficacy of drug-eluting stents (DES). Both late loss and per cent diameter stenosis reliably predict and also fulfil the requirement that between-treatment differences reflect differences in the clinical endpoint, specifically repeat target lesion revascularisation [4646. Mauri L, Orav EJ, Kuntz RE. Late loss in lumen diameter and binary restenosis for drug-eluting stent comparison. Circulation. 2005;111:3435-42. , 4747. Pocock SJ, Lansky AJ, Mehran R, Popma JJ, Fahy MP, Na Y, Dangas G, Moses JW, Pucelikova T, Kandzari DE, Ellis SG, Leon MB, Stone GW. Angiographic surrogate end points in drug-eluting stent trials: A systematic evaluation based on individual patient data from 11 randomized, controlled trials. J Am Coll Cardiol. 2008;51:23-32. , 4848. Leon MB, Nikolsky E, Cutlip DE, Mauri L, Liberman H, Wilson H, Patterson J, Moses J, Kandzari DE. Improved late clinical safety with zotarolimus-eluting stents compared with paclitaxel-eluting stents in patients with de novo coronary lesions: 3-year follow-up from the Endeavor IV (randomized comparison of zotarolimus- and paclitaxel-eluting stents in patients with coronary artery disease) trial. JACC Cardiovasc Interv. 2010;3:1043-50. ]. These angiographic endpoints allow researchers to evaluate the efficacy of new DES rather quickly and with a reasonable degree of certainty in Phase 2 clinical trials with modest sample sizes. Larger studies, including randomised trials and observational studies, can then be performed to ascertain further information about clinical efficacy (e.g., revascularisation) and safety (e.g., stent thrombosis, myocardial infarction and death).

Intention-to-treat vs. per-protocol analysis

In an intent-to-treat analysis (ITT), patients are analysed according to the treatment to which they were assigned, regardless of how they were actually treated. Everyone randomised in the trial is analysed and all of the follow-up information is included in the analysis even if they discontinued the assigned treatment. For superiority trials, intention-to-treat (ITT) analysis is recommended, as this method of analysis preserves the benefit of the underlying randomisation process.

The per-protocol (PP) analysis includes all patients who completed the full course of assigned treatment. In general, the patients who do not comply with therapy and are therefore omitted from a per-protocol analysis are those who are unable to tolerate the treatment or are doing poorly. As a result, the intention-to-treat analysis almost always yields a more conservative estimate of the treatment effect. Hence, a positive result in favour of a new treatment in a properly conducted RCT analysed via intention-to-treat is even more convincing. Most journals and regulatory authorities insist on reporting of the results based on an intention-to-treat analysis.

An unusual situation exists in a non-inferiority study. A per-protocol analysis might in fact be preferable in a non-inferiority design setting, as the intention-to-treat analysis tends to bias towards making the two treatments (new therapy and active control) appear more similar, particularly if unexplained cross-overs exist. In other words, an ITT analysis will often increase the risk of falsely claiming non-inferiority (type I error). Thus, while ITT is more conservative in the usual superiority design, per-protocol analysis tends to be more conservative in a non-inferiority study. However, given the other benefits of an ITT analysis, it is useful to examine both the per-protocol analysis and the intention-to-treat analysis in a non-inferiority trial and there is greater confidence in the results when the conclusions from both analyses are consistent.

The PARTNER trial of transcatheter versus surgical aortic valve replacement in high risk patients is an example of a trial where all randomised patients were analysed according to their allocated groups, regardless of whether they received the treatment for that group [4949. Smith CR, Leon MB, Mack MJ, Miller DC, Moses JW, Svensson LG, Tuzcu EM, Webb JG, Fontana GP, Makkar RR, Williams M, Dewey T, Kapadia S, Babaliaros V, Thourani VH, Corso P, Pichard AD, Bavaria JE, Herrmann HC, Akin JJ, Anderson WN, Wang D, Pocock SJ, PARTNER Trial Investigators. Transcatheter versus surgical aortic-valve replacement in high-risk patients. N Engl J Med. 2011;364:2187–98. ]. Among the 699 patients who were randomly assigned to a study group, 42 did not undergo the assigned procedure (4 in the transcatheter group and 38 in the surgical group), mainly due to withdrawal from the study or a decision not to undergo surgical therapy. Nevertheless, the primary analysis was by intention to treat as required by the regulatory authorities. The primary endpoint of death from any cause was 24.2% in the transcatheter group and 26.8% in the surgical group (p=0.44). The difference of -2.6% (two-sided 95% CI, -9.3 to 4.1; upper limit of the one-sided 95% CI, 3.0%) was within the prespecified non-inferiority margin of 7.5% (p=0.001 for non-inferiority). In addition, as-treated analyses on patients who received the intended treatment were also included in the trial results (death from any cause, 23.7% in transcatheter group vs. 25.2% in surgical group, p=0.64) and showed results consistent with the primary intention to treat analyses, confirming the quality of the results.

Trial monitoring

Monitoring of trial progress is an important component of study implementation. The reasons for monitoring include reporting and evaluation of adverse events, checking for compliance with study protocols and interim analysis of study results according to pre-specified protocol and schedule to look for treatment differences which are sufficiently important to stop the trial.

A Data and Safety Monitoring Board (DSMB) is an independent committee used in clinical trials to monitor the progress of a RCT at regular intervals. The board consists of clinician experts, statisticians and ethicists, and is independent of the investigators and sponsors of the trial. The responsibilities of the board include reviewing interim analyses of outcome data, safety data, major protocol modifications proposed by the investigators during the trial, and reports of concurrent related trials whose results might impact on the continuing merit of the trial. The board then makes recommendations regarding study modification and termination to the study chair and/or sponsor.

Interim analysis

Although the DSMB may recommend terminating a trial based on any concerns of patient safety regardless of the level of statistical significance, planned interim analyses may be pre-specified to ensure that the trial continues only if it remains ethical to assign the study treatments randomly. Interim analyses may be designed to allow for early termination of a trial if the treatments have been shown to be convincingly different at an early stage of enrolment or follow-up, or if there is little chance of a positive outcome (futility).

The endpoint for the interim analysis is pre-specified, as is either the time or enrolment number at which to perform these analyses. The utility and timing of such analyses varies according to the trial design. While there seem to be obvious benefits to conducting interim analyses, there are also significant concerns. The main problem is again that of multiplicity or multiple testing: even if there is no treatment difference, the more often the data are analysed, the greater is the chance of eventually detecting a treatment difference. In other words, if no adjustment is made, the type I error (α) may be increased leading to false-positive findings. If the trial investigators perform interim analysis of the emerging data at α=0.05 at every interim, then the actual level rises with the number of looks, for example, overall α=0.11 after three, α=0.19 after 10 interim analyses.

For this reason, statisticians have developed statistical stopping rules or guidelines for pre-specified interim analysis by prospectively defining p-values or levels of statistical certainty for considering trial termination at an interim analysis while preserving the overall type I error at the 0.05 level. Usually a high level of significance (small p-value) is required for early termination of a trial.

Commonly used methods for adjustment include group sequential designs and are perhaps the easiest to understand and apply. In the fixed nominal approach by Pocock [5050. Pocock SJ. Interim analyses for randomized clinical trials: The group sequential approach. Biometrics. 1982;38:153-62. ], patient entry is divided into a number of equal-sized groups and the decision to stop the trial or continue is based on repeated significance tests of the accumulated data after each group is evaluated. This requires a more stringent “nominal significance level” for each repeated test (e.g., for two interim analyses p=0.029 at each planned analysis, for three interim analyses p=0.022 at each planned analysis, and so on), so that the overall significance level is set at the desired level (usually 0.05). However, the final test of significance is a smaller p-value than that of a regular fixed sample size. If, as in the above example of a trial with three interim analyses, the final test of significance was a p=0.03, the trial would not be deemed significant.

Two other approaches are more commonly used, O’Brien-Fleming and Peto [5151. Schulz KF, Grimes DA. Multiplicity in randomised trials II: Subgroup and interim analyses. Lancet. 2005;365: 1657-61. ]. Both adopt stringent criteria (i.e., low nominal p-values) during the interim analyses which preserve both the α level and the power. The trial can then only be terminated early if the treatment proves greatly superior. The Peto approach uses constant but stringent stopping levels until the final analysis [5151. Schulz KF, Grimes DA. Multiplicity in randomised trials II: Subgroup and interim analyses. Lancet. 2005;365: 1657-61. ]. For instance, in a trial with three interim analyses, the first two interim analyses would have a stopping level of p=0.001 each with the third (final) test of significance at a p=0.05. In the O’Brien-Fleming approach stopping criteria are relatively stringent early on and they successively ease as the results become more reliable and “stable” [5151. Schulz KF, Grimes DA. Multiplicity in randomised trials II: Subgroup and interim analyses. Lancet. 2005;365: 1657-61. ]. Unlike the Peto approach, the O’Brien-Fleming stopping criteria p-values vary with every interval look at the data. For example, in the trial with three interim analyses, with the O’Brien-Fleming stopping criteria, the p-values for the first, second and the third (final) interim analyses would be 0.0005, 0.014 and 0.045, respectively.

Interim analyses should be pre-specified with discussion of the statistical stopping approach in the protocol, in a separate statistical analysis plan, or in a data monitoring committee charter. The confidentiality of any interim analysis is paramount to avoid future bias in the trial. The investigators of the trial and the wider audience, therefore, do not have access to the data and the interim results, if the trial is ongoing. An independent trial statistician, rather than the investigators, should perform the analyses for the data monitoring committee.

Missing data

Missing data are commonly encountered in clinical trials but every effort must be made to follow all patients closely and minimise this as much as possible. Missing data may substantially bias the results of the study, reduce study power, and lead to invalid conclusions. When data are missing at random, that is, due to factors unrelated to the treatment or disease process, then the power of the study is reduced, but this does not introduce bias in the study. However, to assume that data are missing completely at random is usually unrealistic as it is possible that the missing data are related to the treatment or the disease process. For example, patients with missing outcome data may be more likely to be patients who are doing poorly in the study. Thus, when data are missing because of treatment or disease, problems with bias can arise.

Missing data can be handled in a variety of ways during the analysis; however, all methods require an assumption that the data are missing at random. The more commonly described and relatively simple methods include complete-case analysis (excludes observations with missing values for the variable or variables of interest, thus limiting the analysis to those observations for which all values are observed), last observation carried forward (used primarily for analyses of longitudinal studies), and single imputation-based procedures (by assigning the mean or average value to the missing data). Multiple imputation is generally the least biased method and uses the observed values to generate a range of plausible values for each missing value. Apart from using these techniques, it may be important to perform sensitivity analyses to determine the extent of the impact of missing values. A simple method is the “worst case analysis” where the worst is assumed about the missing data – the worst outcome result observed elsewhere in the study is assigned to those patients with missing data. If the qualitative outcome of the study does not change, then one can assume that the conclusion of the study does not depend on the missing data; however, the results from a worst case analysis are recognised often to be unrealistic.

The importance of missing data, excluded cases or lost to follow-up is highlighted by the requirement by some journals that RCT be reported in accordance with the Consolidated Standard of Reporting Trials (CONSORT) statement [44. Moher D, Schulz KF, Altman DG. The CONSORT statement: revised recommendations for improving the quality of reports of parallel-group randomised trials. Lancet. 2001;357:1191-4.
The CONSORT statement provides guidance for the design and reporting of an RCT by use of a checklist and flow diagram depicting information from four stages of a trial (enrolment, intervention allocation, follow-up and analysis). It also enables readers to understand the design, conduct, analysis, and interpretation of an RCT in order to judge its reliability or the relevance of the findings].

Personal perspective - Laura Mauri

Adherence to basic principles of study design is required to ensure the validity and value of a clinical trial. A good clinical study begins with the fundamental question that is to be evaluated, i.e., the study hypothesis. Investigators and clinicians should consider the possible role of bias, confounding, false-positive results and power in the design of a study. Secondary tests may generate new hypotheses for further study. The appropriate design of clinical studies is more than a scientific requirement: it is also an ethical concern, where the proper design of a study ensures that equipoise is present, and that new therapies are evaluated efficiently and conclusively without exposing patients to undue risk.