Fundamentals of coronary biomechanics

Summary

Biomechanical stress plays an important role in vascular disease and this chapter summarises the basic principles of the vascular biomechanical stress state.

One component of this stress state is blood flow induced shear stress. This stress results from frictional forces between blood and the wall. Shear stress is small in magnitude and is mainly sensed by the endothelium. In human coronaries, shear stress can be quantified by combining 3D imaging with computational techniques. These techniques allow us to study the relationship between shear stress, plaque localisation and progression as well as in-stent restenosis.

Other components of the vascular mechanical stress state include wall stresses. These stresses are much larger and are directly related to the deformation of the vessel wall, induced by blood pressure, angioplasty balloons or stents. Constitutive laws are used to describe the relationship between deformation and stress states. Combined with patient-specific images, we can predict the stress state using finite element analysis. Knowing stresses in the wall, we can study blood pressure induced rupture risk as well as the interaction between devices and the diseased vessel wall.

Introduction

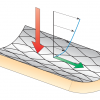
Blood flow transmits forces to the arterial wall which, when normalised by area, are called stresses. The stresses to which the lumen-wall interfaces are exposed can be separated into two components: a stress component that works along the arterial wall in the tangential direction, and a stress component that is directed in an outward or normal direction ( Figure 1 ). The tangential component of the stress is the shear stress induced by the blood flow, and this component is very small in magnitude. The normal component, caused by the blood pressure, is much (up to 4 orders of magnitude) larger.

Shear stress, the tangential component, can only be “sensed” by the endothelium. Shear stress is an important factor that is mainly involved in various mechanisms that regulate the release of vaso-active substances by the endothelium and, along that pathway, shear stress influences the development and progression of atherosclerosis. The magnitude of blood pressure is much larger, and is “sensed” by the complete vessel wall. Deformations induced by shear stress are very small, and can hardly be detected, while blood pressure induces large deformations, which can be fairly easily measured. Generally speaking, shear stress is important for plaque localisation and composition, while blood pressure is the key player in plaque rupture.

All the above mentioned aspects – plaque localisation, progression and rupture – are highly influenced by the biomechanical forces the coronary wall is exposed to, and therefore they are the subjects of an important and active field of research. There is another aspect of vascular biomechanics that is relevant for the clinical setting, and that refers to interventional procedures. Understanding the interaction between the diseased vessel wall and interventional devices – most importantly balloons and stents – is essential for optimisation of design and the clinical outcome of procedures.

In this chapter we will discuss the biomechanical environment that the coronary artery is exposed in the context of atherosclerosis and coronary stents. The heart, the valves, the veins and other equally interesting and important vascular territories in which biomechanical stress plays an important role are not the topic of this particular chapter. Blood flow induced shear stress and blood pressure, and device induced wall stress are addressed separately as they affect different parts of the coronary vessel wall.

Blood flow induced shear stress in coronary arteries

WHAT IS BLOOD FLOW INDUCED SHEAR STRESS?

Definition

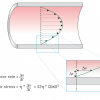
When blood flows through an artery a pressure drop along the artery is required to maintain the flow. This pressure drop is due to the frictional forces exerted on the vessel wall by the blood. Blood flow induced shear stress is the frictional force per unit area, and it is therefore expressed in N/m², or Pa. Shear stress is defined by the product of the velocity gradient at the lumen-wall interface – also called shear rate – and blood viscosity. Shear rate is defined as the velocity difference between two adjacent fluid layers divided by the distance between them ( Figure 2 ).

Let us take a closer look at a simple, but relevant, example: the steady flow of a simple fluid, e.g., water, through a long straight tube. At the wall of the tube, the fluid will stick to the wall, causing very low velocities near it. In the centre of the tube, the velocity will be maximal. In this special case – also known as Poiseuille flow ( Figure 2 ) – we will have a parabolic velocity distribution, and it is from this velocity distribution that we can compute the shear rate at the wall.

Combined with the viscosity of the fluid, we can determine the shear stress according to equation 1:

shear stress = 32 η * Q/πD3 [Pa] (1)

with Q being the flow through the tube, D the diameter of the tube, and η the viscosity of the fluid. When we substitute typical values for coronary blood flow (Q = 60 ml/min, D = 3 mm, η = 3.5 mPa.s), we find that the estimated value of shear stress in coronary arteries is in the order of 1 Pa.

The average blood pressure in the arterial system is approximately 15,000 Pa, which implies that the average shear stress in coronary arteries – and in all other arteries as well – is extremely low compared to blood pressure. Shear stress is therefore only sensed directly by the inner lining of the vessel, the endothelium, and not by the other vessel wall components.

What determines shear stress?

However valuable the work of Poiseuille, it cannot be readily applied to blood flow in large arteries. Obviously, coronary arteries cannot be regarded as long straight tubes. Coronary arteries are characterised by many geometrical features that contradict this assumption, including curved segments, bifurcations, and regions containing stenoses. Even if we assume steady flow and simple fluids, these geometrical features will cause the velocity distribution to deviate from the parabolic one [11. Steinman DA, Vorp DA, Ethier CR. Computational modeling of arterial biomechanics: insights into pathogenesis and treatment of vascular disease. J Vasc Surg. 2003;37:1118-28. ].

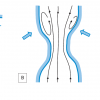
Let us first consider steady flow through a curved segment. Two forces are important if we want to understand the general flow features that can be observed: the centrifugal forces and the forces – or pressure gradient – that is required to change the direction of the flow. The centrifugal forces acting on a particle depend on its velocity: the faster a particle moves, the larger these forces. When a fast moving particle in the centre of the tube enters a curved segment, the centrifugal forces – which are directed towards the outer wall – will push these particles towards the outer wall. The pressure gradient required to change the direction of the flow is rather uniform, and acts from the outer wall towards the inner wall. The result of these two forces is that the fast moving particles move towards the outer wall while the slow moving particles will move towards the inner wall of the curved segment. A swirling motion will be induced resulting in high shear rate –and thus shear stress – along the outer wall of a curved segment, while low shear stress can be expected near the inner wall ( Figure 3 , Panel A). If we look at stenosed segments, the fluid particles flowing through it will first be accelerated due to the lumen narrowing at the upstream part of the stenosis. Generally, this leads to higher shear stresses in the upstream part. In the downstream part, the fluid particles will be decelerated again. The adverse pressure gradient required to decelerate the fluid particles will act in the upstream direction and be fairly uniform across the lumen. Therefore, the slower moving particles near the wall will be decelerated to such an extent that flow reversal may occur, leading to low, and even oscillating, shear stress in the downstream part of the stenosed segment ( Figure 3 , Panel B). Bifurcations add another geometrical feature that induces velocity patterns that deviate from Poiseuille flow: when leaving the mother branch, the flow has to be divided over the two daughter branches. Generally, the faster moving particles from the central part of the flow will impinge on the carina, inducing high shear stresses in those regions. Furthermore, since the flow has to change direction, there will be secondary flow features much like the ones that can be observed in curved segments, inducing a region with low shear stress, and possibly even flow separation, on the hips – or lateral wall – of the bifurcation [22. Ku DN, Giddens DP, Phillips DJ, Strandness DE Jr. Hemodynamics of the normal human carotid bifurcation: in vitro and in vivo studies. Ultrasound Med Biol. 1985;11:13-26. ]. The size of that flow separation region, and the reduction of the shear stress, depend on many factors, including the angle of the bifurcation, the size of the side branch and the flow division.

Another assumption for Poiseuille flow is that we are dealing with a simple fluid, e.g., water. Blood is not a simple fluid, as red blood cells occupy approximately 40% of the total blood volume. Blood can therefore be regarded as a concentrated suspension of flexible particles. The behaviour of blood will differ from simple so-called Newtonian fluids. The most important non-Newtonian feature of blood in the context of the main coronary arteries is that the viscosity depends on the shear rate [44. Gijsen FJ, Allanic E, van de Vosse FN, Janssen JD. The influence of the non-Newtonian properties of blood on the flow in large arteries: unsteady flow in a 90 degrees curved tube. J Biomech. 1999;32:705-13. ]. At higher shear rates, the red blood cells deform and align with the flow, resulting in low viscosity values. At lower shear rates, red blood cells are not deformed or aligned and might even form rouleaux-like structures, leading to an increase in the viscosity. Apart from this so-called shear thinning behaviour (the viscosity of blood reduces with increasing shear rate), blood is slightly viscoelastic, meaning that blood combines viscous and elastic properties. Furthermore, the particulate nature of blood is crucial for various processes near the arterial wall.

Turbulence

The deviations from Poiseuille flow discussed above can induce complex flow fields with swirling flow, stagnation points and flow reversal. These “disturbed” flow fields must not be confused with turbulence. A flow is called turbulent when the velocity of particles is characterised by random fluctuations. Two main requirements have to be met before flow through a tube can be considered turbulent: a dimensionless parameter, the Reynolds number must exceed 2100, and the turbulent structures - being vortices of different sizes - in the flow must have enough time to develop. The Reynolds number is proportional to the average velocity and diameter of the artery and inversely related to viscosity.

The conditions in the coronary circulation are such that the Reynolds number is almost always below 1000, indicating that the conditions for turbulence to occur are not fulfilled. In the rare occasion that the Reynolds number exceeds the threshold value of 2100 (for instance, during exercise with high flow rates in severely occluded coronaries), it will do so only for a brief moment (peak systole), during which turbulent structures do not have enough time to develop. It is therefore highly unlikely that turbulence is present in the coronary circulation. One of the few occasions when turbulence might occur in the arterial circulation is in the aortic arch, immediately downstream of the aortic valve at the moment that they are about to close.

Shear stress in stented segments

Apart from the naturally occurring geometrical variations in the coronary arteries, interventions by stent deployment might also alterflow features and shear stress distribution. It is well known that the deployment of a stent – a relatively stiff structure – in curved arterial segments, changes the overall shape of the segment [55. Wentzel JJ, Whelan MD, van der Giessen WJ, van Beusekom HM, Andhyiswara I, Serruys PW, Slager CJ, Krams R. Coronary stent implantation changes 3-D vessel geometry and 3-D shear stress distribution. J Biomech. 2000;33:1287-95. ]. Due to its stiffness, the stent will induce a straightening effect. This change in overall geometrical features leads to a locally increased curvature at the distal and proximal end of the stent, which in turn lead to local regions of low shear stress and even flow reversal.

Another consequence of treating diseased coronary arteries with a stent can be observed near bifurcations. Depending on the treatment strategy during the intervention, stent struts can potentially cover theostium of the side branch. The blood that has to pass these struts will be hindered by their presence, and flow disturbances will be created [66. Fabregues S, Baijens K, Rieu R, Bergeron P. Hemodynamics of endovascular prostheses. J Biomech. 1998;31: 45-54. ].

Furthermore, during stent deployment, the stent struts may penetrate the arterial wall. Depending on the local properties of the vessel wall tissues, the deployment pressure that was applied, together with the stent design and strut thickness, may cause the struts to partially protrude into the lumen. These protruding stent struts will locally disturb the velocity and shear stress distribution, creating alternating patterns of high and low shear stress. The presence of these patterns was previously demonstrated using computational methods [77. Berry JL, Santamarina A, Moore JE Jr, Roychowdhury S, Routh WD. Experimental and computational flow evaluation of coronary stents. Ann Biomed Eng. 2000; 28:386-98. ], andin vitroexperiments showed a correlation between platelet adhesion and flow disturbances induced by the presence of the stent struts [88. Duraiswamy N, Jayachandran B, Byrne J, Moore JE Jr, Schoephoerster RT. Spatial distribution of platelet deposition in stented arterial models under physiologic flow. Ann Biomed Eng. 2005;33:1767-77. ]. If these patterns are present in human coronary arteries largely depends on how far the stent struts intrude into the lumen, and the presence of these patternsin vivois not convincingly demonstrated.

Finally, after stent deployment, the diameter of the restored lumen in the stent may exceed the proximal diameter of the coronary artery, a phenomena called the step-up( Figure 4 ). This will lead to a sudden expansion of the lumen just downstream of the proximal stent edge. Flow features that can be observed there resemble the ones that we can see downstream of a stenosis: flow recirculation with low shear stress regions can be expected there [99. Thury A, Wentzel JJ, Vinke RV, Gijsen FJ, Schuurbiers JC, Krams R, de Feyter PJ, Serruys PW, Slager CJ. Images in cardiovascular medicine. Focal in-stent restenosis near step-up: roles of low and oscillating shear stress? Circulation. 2002;105:e185-7. ].

In conclusion, the geometrical characteristics of human coronary arteries are responsible for complex flow patterns with swirling flow, flow separation and flow reversal in the main epicardial arteries, and we can therefore expect a heterogeneous shear stress distribution. Low shear stress regions are likely to be present near bifurcations, at the inner bend of curved segments, and immediately distal to a stenosis. Furthermore, turbulence is unlikely to be present in coronary arteries [1010. Steinman DA, Taylor CA. Flow imaging and computing: large artery hemodynamics. Ann Biomed Eng. 2005;33:1704-1709.
This paper presents an overview of the research on the combination of patient derived imaging data and computational
techniques in order to study the relationship between blood flow parameters and arterial diseases, including atherosclerosis and aneurysms.]. Finally, employment of scaffolding devices restores the original arterial lumen and therefore shear stress distribution on a macroscopic scale, but may nevertheless lead to disturbed shear stress patterns locally [1111. Duraiswamy N, Schoephoerster RT, Moreno MR, Moore JE. Stented artery flow patterns and their effects on the artery wall. Annu Rev Fluid Mech. 2007;39:357-82.
The bloodflow related mechanisms which are relevant for various pathological processes after stent placement are discussed with a focus on the influence of stent design on the complex flow patterns.].

SHEAR STRESS AND ATHEROSCLEROSIS

In healthy arteries, the endothelium uses various sensing mechanisms to adapt the vascular dimensions in order to compensate for small changes in flow to maintain a constant shear stress. Let us assume that the flow through a healthy artery increases by 70% due to exercise: This change in flow will be sensed by the endothelium through a simultaneous increase in shear stress. Assuming a steady flow in a straight tube, equation 1 reveals that the diameter of the artery only has to increase by approximately 20% to keep the shear stress constant. This control mechanism was demonstrated convincingly in healthy arteries and it was shown that it can operate in a wide range of flow variations [1212. Zarins CK, Zatina MA, Giddens DP, Ku DN, Glagov S. Shear stress regulation of artery lumen diameter in experimental atherogenesis. J Vasc Surg. 1987;5:413-20. ].

Shear stress in early atherosclerosis

Shear stress also influences endothelial function. Through various pathways, low and oscillating shear stress induces changes in gene expression leading to endothelial dysfunction. This in turn will lead to a pro-atherogenic milieu with an increased endothelial permeability and expression of pro-inflammatory adhesion molecules leading to lipid accumulation followed by an inflammatory response. The low shear stress regions are therefore prone to develop atherosclerosis. In contrast, endothelial cells exposed to normal and high shear stress levels are fully functional, thus creating an atheroprotective environment [1313. Slager CJ, Wentzel JJ, Gijsen FJ, Schuurbiers JC, van der Wal AC, van der Steen AF, Serruys PW. The role of shear stress in the generation of rupture-prone vulnerable plaques. Nat Clin Pract Cardiovasc Med. 2005;2:401-7.
This review discusses the known mechanisms that relate shear stress to plaque formation and growth, with a focus on how these mechanisms might lead to vulnerable plaque formation.]. In the presence of systemic risk factors, low shear stress is generally regarded as one of the key factors responsible for the focal nature of atherosclerosis. This implies that plaques generally originate at the lateral wall of coronary bifurcations [1414. VanderLaan PA, Reardon CA, Getz GS. Site specificity of atherosclerosis: site-selective responses to atherosclerotic modulators. Arterioscler Thromb Vasc Biol. 2004;24:12-22. ].

In the early phase of atherosclerotic disease, the coronary vessel wall is able to undergo positive or compensatory remodelling, thus initially preventing luminal narrowing due to protrusion of the plaque into the lumen. This process is most probably governed by the part of the vessel wall free of plaque, where healthy, functional endothelium is present. This part of the vessel wall will compensate the slight increases in shear stress due to plaque growth. During this process, the region exposed to low shear stress essentially continues to be pro-atherogenic and the plaque will continue to develop. This phenomenon was described by Glagov, and it continues until the plaque occupies approximately 40% of the total vessel area, after which lumen compensation fails [1515. Glagov S, Weisenberg E, Zarins CK, Stankunavicius R, Kolettis GJ. Compensatory enlargement of human atherosclerotic coronary arteries. N Engl J Med. 1987; 316:1371-5. ].

Shear stress in advanced atherosclerosis

The limit to compensatory remodelling is not fully understood: accelerated plaque growth due to intraplaque bleeding or the loss of functionality of the endothelium on the plaque free locations have been suggested, but clinical data to support either hypothesis are scarce. The appearance of plaques in histological images, often with signs of rupture and subsequent healing, points at successive, most probably silent, episodes of plaque growth that might also contribute to lumen narrowing [1616. Burke AP, Kolodgie FD, Farb A, Weber DK, Malcom GT, Smialek J, Virmani R. Healed plaque ruptures and sudden coronary death: evidence that subclinical rupture has a role in plaque progression. Circulation. 2001;103:934-40. ].

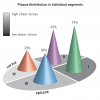
Plaque growth in coronary artery bifurcations was one of the topics that was addressed in a recent observational multislice computer tomography MSCT study [1717. van der Giessen A, Wentzel JJ, Meijboom WB, Mollet NR, van der Steen AFW, van de Vosse FN, de Feyter P, Gijsen FJH. Plaque and shear stress distribution in human coronary bifurcations: a multislice computed tomography study. EuroIntervention. 2009:654-61. ]. In this study, van der Giessen et al observed that early atherosclerotic plaques predominantly are present in the lateral wall of coronary bifurcations; regions that are exposed to low shear stress. However, the plaque location is not limited to the low shear stress region of the bifurcation: a substantial percentage (33%) of the coronary bifurcations also had a plaque near the carina, a region allegedly exposed to high shear stress ( Figure 5 ). However, whenever a plaque was observed in the carina region, there was always plaque in the low shear stress regions as well, indicating that these plaques in human coronary arteries had grown in a circumferential direction. A recent histology study in 26 diseased human coronary artery bifurcations confirm that the lateral wall is more frequently diseased compared to the flow divider wall, and that the plaques found there are larger [1818. Virmani R, Nakazawa G, Yazdani SK, Finn AV, Vorpahl M, Kolodgie FD. Pathological Findings at Bifurcation Lesions The Impact of Flow Distribution on Atherosclerosis and Arterial Healing After Stent Implantation. J Am Coll Cardiol. 2010;55:1679-87. ].

Regardless of the underlying mechanisms, most of the atherosclerotic plaques will at a certain moment encroach on the lumen. The lumen encroachment has far-reaching consequences for the shear stress the plaque is exposed to. As mentioned previously, atherosclerotic plaques originate and develop in low shear stress regions. Once they protrude into the lumen, they reduce the cross sectional area, and the shear stress at the upstream and midcap region increases. The shear stress in the downstream region might even decrease further, thus creating a biomechanical environment that favours plaque progression in the downstream direction.

The endothelium covering a plaque protruding into the lumen is exposed to this change in the shear stress and this will most probably induce a response in the endothelium, subsequently leading to shear stress related changes in plaque composition [1919. Slager CJ, Wentzel JJ, Gijsen FJ, Thury A, van der Wal AC, Schaar JA, Serruys PW. The role of shear stress in the destabilization of vulnerable plaques and related therapeutic implications. Nat Clin Pract Cardiovasc Med. 2005;2:456-64.
The role of shear stress in the more advanced phase of atherosclerosis is still under debate. This paper summarises the relevant mechanisms through which shear stress might influence the composition of lumen intruding vulnerable plaques.].

Shear stress and the vulnerable plaque

A subset of atherosclerotic plaques develops into a plaque phenotype which is often referred to as a thin capped fibro-atheroma. As this type of plaque is prone to rupture, it is also called a vulnerable plaque. This plaque phenotype is characterised by the presence of a large necrotic core, separated from the lumen by a thin fibrous cap, which is often infiltrated by macrophages. Although the plaques typically undergo positive remodelling, they are often lumen narrowing, but not enough to cause any symptoms. Rupture of the thin cap of a vulnerable plaque is thought to be responsible for the majority of acute myocardial infarctions, and occurs when the mechanical stresses in the fibrous cap exceed the strength of the cap. The mechanical stresses in the fibrous cap are induced by blood pressure. Compared to the blood pressure, shear stress is very low in magnitude and therefore has a negligible influence on the mechanical stress in the fibrous cap. However, shear stress does influence endothelial function, even when the endothelium covers a vulnerable plaque. Through its impact on the endothelium, shear stress has an influence on the composition of a vulnerable plaque, thereby influencing the local strength of the cap. In this indirect manner, shear stress can be an important factor for predicting the likelihood of cap rupture.

The downstream part of a plaque will be predominantly exposed to low shear stress. This exposure promotes endothelial dysfunction, in some circumstances even inducing endothelial apoptosis, and both processes will further enhance atherosclerosis in these regions. Not only smooth muscle cell proliferation, but also matrix synthesis will lead to a progression of the disease. Other plaque regions will be exposed to higher shear stress levels. It has been suggested that high shear stress might induce thinning of the fibrous cap along various pathways. Up-regulation of nitric oxide expression might be related to smooth muscle cell apoptosis, leading to a further decrease of cap thickness in high shear stress regions. Matrix regression in high shear stress regions might be mediated by increased endothelial plasmin production. Plasmin might also be important in the up-regulation of matrix metalloproteinase in high shear stress regions. All of these mechanisms suggest that in advanced atherosclerosis the plaque would progress in the low shear stress downstream region, and that the regions exposed to elevated shear stress would be the ones with thinner and weaker caps, predisposed to rupture [1919. Slager CJ, Wentzel JJ, Gijsen FJ, Thury A, van der Wal AC, Schaar JA, Serruys PW. The role of shear stress in the destabilization of vulnerable plaques and related therapeutic implications. Nat Clin Pract Cardiovasc Med. 2005;2:456-64.
The role of shear stress in the more advanced phase of atherosclerosis is still under debate. This paper summarises the relevant mechanisms through which shear stress might influence the composition of lumen intruding vulnerable plaques.].

In conclusion, shear stress influences endothelial function in various ways. In early atherosclerosis, low shear stress is generally regarded as one of the key factors that determines the location of plaque formation [2020. Chatzizisis YS, Coskun AU, Jonas M, Edelman ER, Feldman CL, Stone PH. Role of endothelial shear stress in the natural history of coronary atherosclerosis and vascular remodeling: molecular, cellular, and vascular behavior. J Am Coll Cardiol. 2007;49:2379-93.
An extensive review of the role of shear stress on atherosclerosis, with an emphasis on the known shear stress related molecular and cellular processes. Not only plaque formation and progression, but also vascular remodelling is discussed in depth.]. During the early phase of the disease, outward remodelling prevents the plaque from encroaching into the lumen, and the plaques can continuously develop in the low shear stress regions. When remodelling fails to compensate for plaque growth, the plaque will protrude into the lumen and the shear stress the plaque is exposed to changes [1313. Slager CJ, Wentzel JJ, Gijsen FJ, Schuurbiers JC, van der Wal AC, van der Steen AF, Serruys PW. The role of shear stress in the generation of rupture-prone vulnerable plaques. Nat Clin Pract Cardiovasc Med. 2005;2:401-7.
This review discusses the known mechanisms that relate shear stress to plaque formation and growth, with a focus on how these mechanisms might lead to vulnerable plaque formation.]. The biological impact of this change in shear stress on plaque composition – and therefore plaque vulnerability – are incompletely understood, although plaque regions exposed to high shear stress are likely to be more vulnerable than the regions exposed to low shear stress [1919. Slager CJ, Wentzel JJ, Gijsen FJ, Thury A, van der Wal AC, Schaar JA, Serruys PW. The role of shear stress in the destabilization of vulnerable plaques and related therapeutic implications. Nat Clin Pract Cardiovasc Med. 2005;2:456-64.
The role of shear stress in the more advanced phase of atherosclerosis is still under debate. This paper summarises the relevant mechanisms through which shear stress might influence the composition of lumen intruding vulnerable plaques.].

SHEAR STRESS IN CORONARY ARTERIES

Can we measure shear stress in vivo?

The shear stress can be determined by multiplying the shear rate at the vessel wall with the blood viscosity (see also Figure 2 ). Shear rate is defined as the spatial derivative of the velocity distribution at the wall. In theory, if we can measure the blood flow velocity close to the wall accurately, we can derive the shear rate from measured velocity data. Measuring the velocity of blood in human coronary arteries is difficult due to their small size and the movement of the heart. At this moment, almost all the clinically available devices to measure the blood flow velocity in human coronary arteries in vivo are used to estimate the total flow through the artery. An example of such a device is a Doppler wire. Using an ultrasound beam, a measuring volume is generated that preferentially encompasses the complete lumen of the artery, and all the velocity data in the measured volume are acquired to determine the maximum velocity in the lumen. This maximum velocity, combined with an estimation of the lumen area and an assumption for the velocity profile, is subsequently converted to obtain the total flow through the artery. There is no spatial information available, so we cannot use this device to estimate velocity close to the wall to determine shear rate. There is one device that is able to measure the velocity distribution in human coronary arteries [2121. Lupotti FA, Mastik F, Carlier SG, de Korte CL, van der Giessen WJ, Serruys PW, van der Steen AFW. Quantitative IVUS blood flow: validation in vitro, in animals and in patients. Ultrasound Med Biol. 2003;29:507-15. ]. It combines a standard intravascular ultrasound IVUS catheter with advanced correlation techniques to determine the velocity profile. Apart from the fact that the presence of a catheter disturbs the naturally occurring velocity profile, the spatial resolution of the device is not high enough to accurately determine shear rates at the wall. Since other techniques like magnetic resonance imaging (MRI) measure velocity with an even lower spatial resolution, direct experimental assessment of local shear stress distribution in human coronary arteries is currently not feasible.

How can we compute shear stress?

An alternative approach to determine the shear stress distribution in human coronary arteries relies on the combination of imaging techniques and computational fluid dynamics (CFD). The imaging techniques are required to determine the 3D geometry of the coronary artery. The acquired geometrical data is then fed into a CFD software program to compute the velocity and shear stress distribution instead of measuring it.

The most important input for the CFD is the 3D geometry of the lumen of the coronary artery. The most accurate technique available is called ANGUS, which is a combination of IVUS and biplane angiography [2222. Slager C, Wentzel J, Schuurbiers J, Oomen J, Krams R, Achterberg H, Kloet J, de Feyter P. True 3-D reconstruction of coronary arteries in patients shows accurate correspondence between X-ray and IVUS derived dimensions. Circulation. 1998;98:I 508. ]. The contours of the lumen and the outer wall can be delineated accurately in the IVUS images. The information of the biplane angiographic data is then used to determine the 3D position of each IVUS image and the corresponding lumen contours. This procedure was validated and used by several groups to compute the shear stress in human coronary arteries ( Figure 6 ). MSCT angiographic data can serve as an alternative to the biplane angiographic data for determining the 3D position of the IVUS images ( Figure 7 ).

Other studies do not rely on IVUS for the generation of the contours, but use angiographic data only or use MSCT angiography or MRI to generate the 3D lumen of coronary arteries [2323. van der Giessen A, Schaap M, Gijsen F, Groen H, van Walsum T, Mollet N, J D, van de Vosse F, Niessen W, de Feyter P, van der Steen A, Wentzel J. 3D fusion of intravascular ultrasound and coronary computed tomography for in-vivo wall shear stress analysis – a feasibility study. Int J Cardiovasc Imaging. 2010;26:781-96. ]. The main limitation of these last studies is the poor resolution of the applied imaging modalities.

Apart from geometrical data, the CFD software requires additional parameters, the most important being the flow rate through the artery. The flow rate through the artery can be obtained from invasive flow measurements (see above), but empirical relationships that relate local diameter to flow can also be used.

After converting the geometrical information into a computational mesh and solving the governing equations, the shear stress distribution can be mapped onto the luminal surface. If the shear stress data are combined with other – preferably functional – parameters, the relationship between shear stress and atherosclerotic plaque development can be investigated.

SHEAR STRESS IN CLINICAL STUDIES

In one of the first studies that employed the ANGUS method, Krams et al [2424. Krams R, Wentzel J, Oomen J, Vinke R, Schuurbiers J, de Feyter P, Serruys P, Slager C. Evaluation of endothelial shear stress and 3D geometry as factors determining the development of atherosclerosis and remodeling in human coronary arteries in vivo. Combining 3D reconstruction from angiography and IVUS (ANGUS) with computational fluid dynamics. Arterioscler Thromb Vasc Biol. 1997;17:2061-5. ] investigated the relationship between shear stress and vessel wall thickness in the right coronary artery. Data on vessel wall thickness were derived from IVUS and considered as a marker for the presence of an atherosclerotic plaque. They demonstrated an inverse relationship between shear stress and wall thickness: thicker plaques were observed in regions exposed to the lowest shear stress.

This observation was confirmed by the work from Stone et al [2525. Stone PH, Coskun AU, Kinlay S, Clark ME, Sonka M, Wahle A, Ilegbusi OJ, Yeghiazarians Y, Popma JJ, Orav J, Kuntz RE, Feldman CL. Effect of endothelial shear stress on the progression of coronary artery disease, vascular remodeling, and in-stent restenosis in humans: in vivo 6-month follow-up study. Circulation. 2003;108:438-44. ] who studied plaque localisation and progression over a 6 month period. They demonstrated that regions exposed to low shear stress at baseline showed a significant increase in wall thickness. This increase in wall thickness was accompanied by an increase in the external elastic membrane dimensions such that lumen dimensions remained unaltered. Regions exposed to higher shear stress additionally underwent outward remodelling leading to a normalisation of shear stress values.

Wentzel et al [2626. Wentzel JJ, Janssen E, Vos J, Schuurbiers JC, Krams R, Serruys PW, de Feyter PJ, Slager CJ. Extension of increased atherosclerotic wall thickness into high shear stress regions is associated with loss of compensatory remodeling. Circulation. 2003;108:17-23. ] investigated the relationship between shear stress and wall thickness in the angiographically normal segments of human coronary arteries of 14 patients. Based on the area stenosis, the segments were divided into segments with lumen preservation and segments with lumen narrowing. The previously reported inverse relationship was observed for the segments with lumen preservation, however, not for the segments with lumen narrowing, indicating that the processes related to protrusion of the plaque into the lumen are not regulated by shear stress.

Instead of using IVUS derived wall thickness data as a marker for atherosclerosis, one can use other imaging parameters as well. Gijsen et al [2727. Gijsen FJH, Wentzel JJ, Thury A, Mastik F, Schaar JA, Schuurbiers JCH, Slager CJ, van der Giessen WJ, de Feyter PJ, van der Steen AFW, Serruys PW. Strain distribution over plaques in human coronary arteries relates to shear stress. American Journal of Physiology - Heart and Circulatory Physiology. 2008;295:H1608-14. ] applied an intravascular ultrasound technique, called palpography (see also section “How can we measure vessel wall strain”), that can measure the strain distribution in the vessel wall layer adjacent to the lumen. Strain can be considered as a surrogate marker for plaque composition. Ex vivo experiments have shown that high strain values are associated with increased macrophage accumulation, low smooth muscle cell content and thin fibrous caps. In contrast, low strain values indicate the presence of stiff wall material and are related to high smooth muscle cell content. In 13 coronary arteries, 31 plaques were identified. These plaques were divided into 4 regions: the upstream, midcap, downstream and shoulder region. The downstream region was exposed to low shear stress, and strain values were lower there, indicating that more smooth muscle cells are present downstream of a plaque. The other regions could not be separated based on shear stress or strain values. However, plaque regions exposed to the highest shear stress levels revealed the highest strain, indicating that those regions are weaker. In a subset of this patient group, 6 month follow-up strain data was available as well [2828. Gijsen FJ, Mastik F, Schaar JA, Schuurbiers JC, van der Giessen WJ, de Feyter PJ, Serruys PW, van der Steen AF, Wentzel JJ. High shear stress induces a strain increase in human coronary plaques over a 6-month period. EuroIntervention. 2001;7:121-7. ]. It was seen that regions exposed to the highest shear stress showed an increase of strain, suggesting that those plaque regions got weaker over time. These results imply that high shear stress might induce patho-biological responses in the more advanced phases of atherosclerosis that lead to enhanced plaque vulnerability.

These findings are in keeping with another study in which the relationship between shear stress and plaque composition derived from virtual histology intravascular ultrasound was investigated [2929. Samady H, Eshtehardi P, McDaniel MC, Suo J, Dhawan SS, Maynard C, Timmins LH, Quyyumi AA, Giddens DP. Coronary artery wall shear stress is associated with progression and transformation of atherosclerotic plaque and arterial remodeling in patients with coronary artery disease. Circulation. 2011;124:779-88. ]. It was observed that plaque regions exposed to low shear stress showed an increase of plaque area over a 6-month period, with a significant increase in necrotic core area. The high shear stress regions demonstrated a decrease in plaque area, which was associated with an increase in necrotic core region and a regression of fibrous and fibrofatty tissue components, suggesting that the high shear stress regions are more vulnerable.

Rupture of the vulnerable plaque can lead to events and therefore represents the most relevant phase of atherosclerosis for the patient. Rupture occurs at the location where the cap is the weakest, and the previously discussed studies indicate that shear stress might be one of the factors that influences cap strength. High shear stress might be involved in various processes that locally increase vulnerability, a finding that was confirmed in two recent studies. Fukumoto et al [3030. Fukumoto Y, Hiro T, Fujii T, Hashimoto G, Fujimura T, Yamada J, Okamura T, Matsuzaki M. Localized elevation of shear stress is related to coronary plaque rupture: a 3-dimensional intravascular ultrasound study with in-vivo color mapping of shear stress distribution. J Am Coll Cardiol. 2008;51:645-50. ] applied IVUS to determine the location of plaque rupture in culprit lesions. They qualitatively associated the location of plaque rupture in the lumen narrowing lesions with locally elevated shear stress levels. They demonstrated that the location of plaque rupture was found predominantly in the upstream shoulder regions and that the rupture location was, on average, exposed to higher shear stress levels than the plaque.

Shear stress is associated with various markers of atherosclerotic disease not only in untreated arteries but also after stent placement, which was convincingly demonstrated in an animal study by Carlier et al using rabbits [3131. Carlier SG, van Damme LC, Blommerde CP, Wentzel JJ, van Langehove G, Verheye S, Kockx MM, Knaapen MW, Cheng C, Gijsen F, Duncker DJ, Stergiopulos N, Slager CJ, Serruys PW, Krams R. Augmentation of wall shear stress inhibits neointimal hyperplasia after stent implantation: inhibition through reduction of inflammation. Circulation. 2003;107:2741-6. ]. They introduced a stent with a flow divider in the centre in one of the iliac arteries, and a stent without the flow divider in the other iliac artery. The flow divider induced a twofold increase in shear stress in the stent. It was shown that the increased shear stress levels lead to a decrease in neointima hyperplasia and a decrease of inflammation.

Wentzel et al [3232. Wentzel JJ, Krams R, Schuurbiers JC, Oomen JA, Kloet J, van Der Giessen WJ, Serruys PW, Slager CJ. Relationship between neointimal thickness and shear stress after Wallstent implantation in human coronary arteries. Circulation. 2001;103:1740-5. ] used the previously discussed 3D reconstruction technique to investigate the relationship between shear stress and neointima hyperplasia in self-expanding stents in 14 human coronary arteries. They found that after a 6-month period, the neointimal hyperplasia was more profound in the low shear stress regions. These findings were not confirmed by Stone et al for balloon-expandable stents in a smaller patient population [2525. Stone PH, Coskun AU, Kinlay S, Clark ME, Sonka M, Wahle A, Ilegbusi OJ, Yeghiazarians Y, Popma JJ, Orav J, Kuntz RE, Feldman CL. Effect of endothelial shear stress on the progression of coronary artery disease, vascular remodeling, and in-stent restenosis in humans: in vivo 6-month follow-up study. Circulation. 2003;108:438-44. ]. Finally, in drug-eluting stents, an inverse relation between shear stress and neointima thickness was found by Gijsen et al [3333. Gijsen FJ, Oortman RM, Wentzel JJ, Schuurbiers JC, Tanabe K, Degertekin M, Ligthart JM, Thury A, de Feyter PJ, Serruys PW, Slager CJ. Usefulness of shear stress pattern in predicting neointima distribution in sirolimus-eluting stents in coronary arteries. Am J Cardiol. 2003;92:1325-8. ]. In that study it was shown that stent regions exposed to higher shear stress at baseline were associated with tissue regression at 6-month follow-up.

In conclusion, due to the movement of the heart and the size of the coronary arteries, direct non-invasive imaging of shear stress is not currently feasible. Application of invasive 3D imaging to obtain the shape of the coronary in combination with computational methods is the most reliable way to determine shear stress. Using these methods it was shown that shear stress could be associated with various markers of atherosclerosis in human coronary arteries. It was demonstrated that locations exposed to low shear stress are most frequently affected by atherosclerotic disease. Plaques protruding into the lumen are exposed to locally elevated shear stress levels, and these regions are associated with enhanced vulnerability. In segments implanted with stents, decreased shear stress is associated with patterns of in-stent restenosis.

Coronary vessel wall mechanics

WHAT IS VESSEL WALL STRESS AND STRAIN, AND HOW ARE THEY LINKED?

The concepts of stress and strain can be understood by studying a simple tensile test as shown in Figure 8 . Applying a tensile force (F) to a vessel specimen with initial cross-sectional area Ao and length lo increases the specimen length by Δl. This Δl is length dependent since a larger length change will be obtained when a specimen with a longer initial length is subjected to the same force. However, the deformation per unit of length (Δl/l), called strain (ε), is independent of the specimen length. Therefore, strain is often used to characterise the deformation of a physical body under the action of applied forces. Similarly, stress (σ), defined as force per unit of area (F/A), is used to describe the intensity of the internal forces within a physical body. The unit of stress is Pa = N/m², while strain is dimensionless.

Stress and strain are related, however, the relationship is dependent on the type of specimen. Many materials display an elastic behaviour at small strains, meaning that the material returns to its original shape after the external forces that made it deform are removed. Some materials have a linear stress-strain relation within the elastic limit ( Figure 9 , Panel A) and are therefore called linear elastic or Hookean materials. In these cases, Hooke’s law can be used, σ = E.ε, where E is a material constant called Young’s modulus. Young’s modulus is an intrinsic measure of material stiffness with the same unit as stress, Pa. A material with a higher Young’s modulus (and thus stiffness) requires a larger stress to obtain a certain strain. Steel is a typical example of a material exhibiting linear elastic behaviour for small strains, which are common in many engineering applications. Young’s modulus for steel is typically about 200 MPa.

When a specimen is stretched in one direction, it usually tends to contract in the other two directions perpendicular to the direction of extension. This phenomenon is called the Poisson effect. Poisson’s ratio (ν) is defined as the negative of the ratio of the transverse strain to the axial strain resulting from a loading in the axial direction, and is a measure of the Poisson effect (ν = –ε_transverse/ε_axial). Incompressible materials that do not change their volume when subjected to external forces, as appears to be the case for most biological tissues, have a Poisson ratio of 0.5.

Soft biological material such as arterial tissue typically has a complex mechanical behaviour that is determined by the tissue composition (see, for example reference [3434. Humphrey JD. Cardiovascular solid mechanics. Cells, tissues and organs. 2002 Springer, New York.
This book provides a general introduction to soft tissue biomechanics.]). This composition is different for each arterial layer (intima, media and adventitia), and hence, also the mechanical behaviour of each layer differs. Therefore, it is said that arterial tissue is a heterogeneous material. In general, arterial tissue can be considered as a fibre-rein forced composite structure, with collagen, elastin and smooth muscle cells being the main constituents. The impact of this composition on mechanical behaviour can easily be explained by studying a representative stress-strain curve for arterial tissue under tension ( Figure 9 , Panel B). Arterial tissue typically exhibits a nonlinear elastic behaviour as reflected by the J-shaped curve. The slope of the curve increases with increasing strain, meaning that the arterial tissue becomes stiffer as the deformations get larger. In this way, overstretching of blood vessels is avoided. At small deformations (phase I in Panel B of Figure 9 ), the collagen fibres appear wavy and bear no load. Low stresses lead to large deformations of the collagen fibres without requiring stretch of the fibres. In this phase, elastin is mainly responsible for the elastic behaviour of the tissue, and the relation between stress and strain can initially be approximated as linear. As the load increases, the collagen fibres unfold and the stiffness of the material increases (phase II in panel B of Figure 9 ). At high tensile stresses, the wavy pattern disappears and the collagen fibres straighten and resist the load strongly (phase III in panel B of Figure 9 ). In this phase, the stress-strain relation again becomes more or less linear.

The collagen fibres within arterial tissue have preferred orientations leading to a mechanical behaviour that is directionally dependent. In other words, the stress-strain relationship of vascular tissue in the longitudinal direction differs from the relationship in the circumferential direction. Such directionally dependent behaviour is called anisotropy, as opposed to isotropy. A schematic representation of this anisotropic behaviour is shown in Panel C of Figure 9 .

OTHER MECHANICAL CHARACTERISTICS OF VASCULAR TISSUE

Besides the heterogeneity, nonlinearity and anisotropy, there are additional aspects that further determine the mechanical properties of vascular tissue. Like blood, vascular tissue demonstrates viscoelastic properties. The term viscoelasticity is used for materials that exhibit both elastic and viscous (or fluid-like) characteristics when undergoing deformations. Applying a certain stress to a viscous material leads to deformations that evolve with time. The most important viscoelastic properties of arterial tissue are creep, stress relaxation and hysteresis. Creep is the tendency of a material to slowly deform under the influence of a fixed stress, while stress relaxation is used to describe the fact that the stress within the material decreases when a constant stretch is applied. Cyclic loading of arterial tissue leads to a hysteresis loop when plotting stress versus strain. This means that the stress-strain path during loading differs from the one during unloading.

Observations revealed that arteries usually shorten when transected, thus suggesting the existence of an axial prestretch in vivo. Average values of 5% prestretch have been reported for aged non-diseased coronary arteries with respect to the load-free length [3535. Holzapfel GA, Sommer G, Gasser CT, Regitnig P. Determination of layer-specific mechanical properties of human coronary arteries with nonatherosclerotic intimal thickening and related constitutive modeling. Am J Physiol Heart Circ Physiol. 2005;289:H2048-H2058.
In this paper; the mechanical behaviour of postmortem coronary tissue samples is analysed and a constitutive model is proposed that can be used when modelling coronary artery tissue.]. However, in some cases, the vessel may elongate axially after excision. It was also shown that axial prestretch increases with age during postnatal development [3434. Humphrey JD. Cardiovascular solid mechanics. Cells, tissues and organs. 2002 Springer, New York.
This book provides a general introduction to soft tissue biomechanics.]. This observation has been partially attributed to stretching of the vessels by growth.

One very interesting property of vascular tissue is the fact that removal of all external loads (longitudinal stretch and blood pressure) does not lead to a stress-free state. The stresses that are still present within the tissue are called residual stresses. The classical way to demonstrate the presence of these residual stresses is to excise a cylindrical segment (ring) of a blood vessel and to make a radial cut [3434. Humphrey JD. Cardiovascular solid mechanics. Cells, tissues and organs. 2002 Springer, New York.
This book provides a general introduction to soft tissue biomechanics.]. The vessel specimen will not maintain its cylindrical shape and will “open up” ( Figure 10 , Panel A). This opening implies that the inner wall of the intact unloaded ring is in compression and the outer wall is in tension (see Panel B in Figure 10 ). Quantification of this opening is usually done by measuring the so-called opening angle θ (see Panel A of Figure 10 ). However, it has been demonstrated that a single radial cut is not sufficient to relieve all residual stresses. A more advanced approach to investigate and quantify residual stresses is to separate the individual arterial layers (intima, media and adventitia) and to study both cylindrical portions as well as longitudinal strips [3636. Holzapfel GA, Sommer G, Auer M, Regitnig P, Ogden RW. Layer-specific 3D residual deformations of human aortas with non-atherosclerotic intimal thickening. Ann Biomed Eng. 2007;35:530-45. ].

Residual stresses play an important role in maintaining a fairly uniform stress distribution across the arterial wall at physiological loads as illustrated in Figure 10 , Panel C. In contrast, if residual stresses would not be present, normal blood pressures would cause much higher stresses and strains at the intimal side of the vessel wall as compared to the adventitial side.

MEASURING AND MODELLING TISSUE ELASTICITY

In the previous section, the mechanical properties of vascular tissue were described in a qualitative manner. Based on these general observations, theoretical models can be formulated which have a predictive capability. Such models are then employed to investigate the mechanics of arteries and, for example, the interaction with medical devices, often via numerical simulations. However, quantitative experimental information regarding the mechanical behaviour of arteries is required to calibrate these models which usually contain several model parameters. Such quantitative information is obtained through a number of dedicated experiments.

A common experiment to quantify the stress-strain behaviour of vascular tissue is to clamp a tissue strip at its two ends, stretch it in one direction, and measure the resulting forces (i.e., uniaxial tensile test). This can be done for the complete vessel wall, or alternatively, for each arterial layer separately. The anisotropic properties of the tissue can be quantified by performing uniaxial tensile tests in both the circumferential and the longitudinal direction. In-plane biaxial testing on rectangular specimens, clamped at the four edges, can also be performed. This experiment requires and advanced set-up as loads and deformations need to be controlled and monitored in two directions. A third type of test, called the inflation-extension test, uses tubular specimens instead of tissue strips. During this test, the tubular section is pressurised and stretched in axial direction, while the diameter and length of the sample are measured.

As already mentioned, the information obtained experimentally can serve as input to calibrate a theoretical model that can then describe the mechanical behaviour of arterial tissue in a quantitative way. A linear elastic material model cannot be used as the arterial wall behaves strongly nonlinearly, especially when subjected to large strains. A better approximation of the non-linear stress-strain behaviour of arterial tissue can be obtained by assuming the existence of a strain energy function, from which the stress can be computed by differentiation with respect to strain. A material defined in this way is called hyperelastic. Different types of hyperelastic models or strain energy functions have been proposed for both isotropic and anisoptropic materials. A detailed description of these advanced material models is beyond the scope of this chapter, but the interested reader is referred to, for example, Holzapfel et al [3535. Holzapfel GA, Sommer G, Gasser CT, Regitnig P. Determination of layer-specific mechanical properties of human coronary arteries with nonatherosclerotic intimal thickening and related constitutive modeling. Am J Physiol Heart Circ Physiol. 2005;289:H2048-H2058.
In this paper; the mechanical behaviour of postmortem coronary tissue samples is analysed and a constitutive model is proposed that can be used when modelling coronary artery tissue.].

STRESS AND STRAIN IN CORONARY ARTERIES

How can we image vessel wall strain?

While intra-arterial stresses or stress within plaques cannot be assessed directly, there are some techniques available that allow their indirect estimation by measuring deformation or strain. Anticipated strain values are in the order of a few percentages, which, given the small dimensions of the coronary artery wall (~1 mm), requires techniques with high spatial as well as temporal resolution. To the best of our knowledge, the only technique that fulfils these prerequisites and which currently has a practical applicability in the clinic is high-frequency ultrasound [3737. Cespedes EI, de Korte CL, van der Steen AFW. Intraluminal ultrasonic palpation: Assessment of local and cross-sectional tissue stiffness. Ultrasound Med Biol. 2000;26:385-96. , 3838. de Korte CL, Carlier SG, Mastik F, Doyley MM, van der Steen AFW, Serruys PW, Bom N. Morphological and mechanical information of coronary arteries obtained with intravascular elastography - Feasibility study in vivo. Eur Heart J. 2002;23:405-13.
This paper describes how intravascular imaging can be employed to get information about the tissue elasticity., 3939. de Korte CL, van der Steen AFW. Intravascular ultrasound elastography: an overview. Ultrasonics. 2002; 40:859-65. , 4040. de Korte CL, van der Steen AFW, Cespedes EI, Pasterkamp G, Carlier SG, Mastik F, Schoneveld AH, Serruys PW, Bom N. Characterization of plaque components and vulnerability with intravascular ultrasound elastography. Phys Med Biol. 2000;45:1465-75. , 4141. Saijo Y, Tanaka A, Iwamoto T, dos Santos Filho E, Yoshizawa M, Hirosaka A, Kijima M, Akino Y, Hanadate Y, Yambe T. Intravascular two-dimensional tissue strain imaging. Ultrasonics. 2006;44:E147-E151. ]. However, as the penetration depth in tissue of ultrasound is limited and inversely related to the applied frequency, strain measurements are only confined to invasive catheter-based ultrasound imaging modalities (IVUS), with applied ultrasound frequencies in the order of 20 MHz.

Without going into technical detail, methods to measure strain make use of the captured raw ultrasound signals reflected from the tissue (RF or radio-frequency data), and cross-correlation techniques are used to assess the tissue deformation from one image frame to the next one [3737. Cespedes EI, de Korte CL, van der Steen AFW. Intraluminal ultrasonic palpation: Assessment of local and cross-sectional tissue stiffness. Ultrasound Med Biol. 2000;26:385-96. ]. This also implies that to measure deformation the loading conditions of the tissue vary from one frame to the other. In vivo, these different loading conditions are generated by the arterial pulse, cyclically loading the arteries from diastolic to systolic pressure. Inherent to the technique, however, is that the information embedded in subsequent image frames is correlated. This is not trivial in the setting of coronary IVUS, where cardiac motion has a strong impact on the position of the catheter, hampering the methodology [4242. Danilouchkine MG, Mastik F, van der Steen AFW. Improving IVUS Palpography by Incorporation of Motion Compensation Based on Block Matching and Optical Flow. IEEE Trans Ultrason Ferroelectr Freq Control. 2008;55:2392-404. ]. For this reason, one often limits the measurements to image frames recorded in end-diastole, when cardiac motion is minimal. The drawback, however, is also that the change in loading conditions is fairly limited (to the order of 5 mmHg), yielding low absolute values of strain (max. 1-2%). Nevertheless, the technique is mainly applied to assess relative differences in strain to identify zones of large (normal tissue, soft plaque) and small deformations (hard plaque). This information, together with grey-scale B-mode images as well as other techniques such as virtual histology and analysing the ultrasonic fingerprint of the different wall constituents, allows for assessment of the arterial wall and should contribute to the assessment of risk of rupture of coronary plaques [4040. de Korte CL, van der Steen AFW, Cespedes EI, Pasterkamp G, Carlier SG, Mastik F, Schoneveld AH, Serruys PW, Bom N. Characterization of plaque components and vulnerability with intravascular ultrasound elastography. Phys Med Biol. 2000;45:1465-75. ]. As the method is confined to the inner layer of the coronary artery and visualises differences in stiffness, similar to what one would feel if one were to palpate the intima of the artery, the technique is also referred to as palpography (see Figure 11 ).

An important consideration is the fact that IVUS catheters emit ultrasound waves in the radial direction, and that the basic technique thus only allows the measurement of the radial strain component. It has, however, been shown that it is possible to measure 2D strain providing estimates of both the radial as well as circumferential strain [4141. Saijo Y, Tanaka A, Iwamoto T, dos Santos Filho E, Yoshizawa M, Hirosaka A, Kijima M, Akino Y, Hanadate Y, Yambe T. Intravascular two-dimensional tissue strain imaging. Ultrasonics. 2006;44:E147-E151. , 4343. Friedman MH, Liang Y, Zhu H, Gehrig T. Measurement of the transverse strain tensor in the coronary arterial wall from clinical intravascular ultrasound images. J Biomech. 2008;41:2906-11. ], and 3D techniques are being studied [4444. Liang Y, Zhu H, Friedman MH. Measurement of the 3D arterial wall strain tensor using intravascular B-mode ultrasound images: a feasibility study. Phys Med Biol. 2010;55:6377-94. ]. Given the 3D nature of the coronary arteries and their deformation, it is anticipated that these novel techniques will provide a more complete picture of the biomechanics of the coronary artery and its constituents.

How can we compute vessel wall strain?

Complementary to ultrasound-based strain measurements, the vessel stress/strain state can also be studied using a computational technique called Finite Element Analysis (FEA). Briefly stated, FEA is the investigation by numerical means of the mechanics of physical systems. The continuum (e.g.. the vessel wall) is divided into a finite number of discrete regions, named elements, whose behaviour can be described mathematically. An approximate solution of the entire continuum is solved from the assembly of the individual elements. Usually, the displacements of the nodes are taken as the fundamental unknown quantities and from the displacements, the strains are evaluated by taking the appropriate derivatives. The material constitutive behaviour provides the necessary basis for computing stress levels from these strains. Thus, FEA essentially transforms the unknowns from the various continuous fields into equations of discrete nodal quantities. Assuming that certain basic numerical requirements and standards of practice are satisfied, the solution obtained from the FEA estimates the exact physical solution.

In general, a finite element model is defined by its geometry, material properties, and some appropriate loading and boundary conditions mimicking the targeted real life situation. As an example, nowadays, FEA can be used to assess the stress state during a coronary bifurcation stenting procedure (see Figure 12 ). Depending on the aim of the simulations, the coronary bifurcation model can be created using computer-aided design tools or based on patient specific geometrical data obtained from medical images (CT, ultrasound, MRI, etc.). The material behaviour can include anisotropy for the intima, media and adventitia, or simplify the complete coronary vessel wall to one isotropic medium. However, one should always keep in mind that such computer models are based on a number of assumptions. Therefore, considerable effort should be put into the validation of these models using experimental (in vitro and/or in vivo) data.

CLINICAL PERSPECTIVES OF WALL STRESS ANALYSIS

Wall stress analysis of aneurysms

One of the most studied problems in the field of cardiovascular biomechanics is the stress analysis of cerebral and abdominal aortic aneurysms [4545. Fillinger MF, Marra SP, Raghavan ML, Kennedy FE. Prediction of rupture risk in abdominal aortic aneurysm during observation: Wall stress versus diameter. J Vasc Surg. 2003;37:724-32. , 4646. Fillinger MF, Raghavan ML, Marra SP, Cronenwett JL, Kennedy FE. In vivo analysis of mechanical wall stress and abdominal aortic aneurysm rupture risk. J Vasc Surg. 2002;36:589-97. , 4747. Ma B, Lu J, Harbaugh RE, Raghavan ML. Nonlinear anisotropic stress analysis of anatomically realistic cerebral aneurysms. J Biomech Eng. 2007;129:88-96. , 4848. Rodriguez JF, Ruiz C, Doblare M, Holzapfel GA. Mechanical stresses in abdominal aortic aneurysms: Influence of diameter, asymmetry, and material anisotropy. J Biomech Eng. 2008;130. , 4949. Torii R, Oshima M, Kobayashi T, Takagi K, Tezduyar TE. Computer modeling of cardiovascular fluid-structure interactions with the deforming-spatial-domain/stabilized space-time formulation. Computer Methods in Applied Mechanics and Engineering. 2006;195:1885-95. , 5050. Vorp DA, Raghavan ML, Webster MW. Mechanical wall stress in abdominal aortic aneurysm: Influence of diameter and asymmetry. J Vasc Surg. 1998;27:632-9. , 5151. Vorp DA. Biomechanics of abdominal aortic aneurysm. J Biomech. 2007;40:1887-902.
This review gives an overview of different aspects of stress analysis within abdominal aortic aneurysms.]. As aneurysm rupture is, in essence, a mechanical failure of the tissue where load becomes higher than the strength of the material, it makes sense that the biomechanical analysis of the risk of rupture might provide additional diagnostic information beyond simple and quite crude clinical criteria such as the diameter of the aneurysm (5.5 cm for abdominal aortic aneurysms) or its growth rate [5252. Lobato AC, Puech-Leao P. Predictive factors for rupture of thoracoabdominal aortic aneurysm. J Vasc Surg. 1998;27:446-53. , 5353. Moxon JV, Parr A, Emeto TI, Walker P, Norman PE, Golledge J. Diagnosis and Monitoring of Abdominal Aortic Aneurysm: Current Status and Future Prospects. Curr Probl Cardiol. 2010;35:512-48. ]. Several studies have demonstrated the feasibility of calculating wall stress on a semi patient-specific basis, making use of numerical finite element methods [5454. Castro MA, Putman CM, Cebral JR. Patient-specific computational modeling of cerebral aneurysms with multiple avenues of flow from 3D rotational angiography images. Acad Radiol. 2006;13:811-21. , 5555. Raghavan ML, Vorp DA. Toward a biomechanical tool to evaluate rupture potential of abdominal aortic aneurysm: identification of a finite strain constitutive model and evaluation of its applicability. J Biomech. 2000;33:475-82. , 5656. Vande Geest JP, Wang DHJ, Wisniewski SR, Makaroun MS, Vorp DA. Towards a noninvasive method for determination of patient-specific wall strength distribution in abdominal aortic aneurysms. Ann Biomed Eng. 2006;34:1098-106. , 5757. Wang DHJ, Makaroun MS, Webster MW, Vorp DA. Effect of intraluminal thrombus on wall stress in patient-specific models of abdominal aortic aneurysm. J Vasc Surg. 2002;36:598-604. , 5858. Wolters B, Rutten MCM, Schurink GWH, Kose U, de Hart J, van de Vosse FN. A patient-specific computational model of fluid-structure interaction in abdominal aortic aneurysms. Med Eng Phys. 2005;27:871-83. ].

Today, it is perfectly possible to segment the arterial lumen, and even the thrombus, from medical images (MRI or CT). This might form a sufficient basis for calculation of intra-arterial flow fields and assessment of the shear stress exerted by the blood flow, but it is insufficient for structural analyses. Structural analyses requires additional information including the thickness of the arterial wall, the constitutive laws describing its behaviour as well as the stress conditions of the unloaded aneurysm and thrombus. Each of these issues are at present unresolved and the non-exhaustive list below briefly addresses some of them:

• Current imaging techniques do not possess the spatial resolution or appropriate scan sequences required to resolve the arterial wall. As such, in many studies, default values are used for the thickness of the arterial wall (e.g., 2 mm or a fixed ratio between wall thickness and lumen diameter).
• As the arterial wall is a multi-layered structure, complex in organisation and nonlinear in the behaviour of its individual constituents (e.g., collagen) and, as a whole, accurate constitutive laws can be complex, requiring values for multiple parameters, which need to be assessed in one way or another from the available data. At present, computations are done using data gathered from a limited set of tests done on tissue samples [3535. Holzapfel GA, Sommer G, Gasser CT, Regitnig P. Determination of layer-specific mechanical properties of human coronary arteries with nonatherosclerotic intimal thickening and related constitutive modeling. Am J Physiol Heart Circ Physiol. 2005;289:H2048-H2058.
  In this paper; the mechanical behaviour of postmortem coronary tissue samples is analysed and a constitutive model is proposed that can be used when modelling coronary artery tissue., 5959. Gasser TC, Ogden RW, Holzapfel GA. Hyperelastic modelling of arterial layers with distributed collagen fibre orientations. J R Soc Interface. 2006;3:15-35. , 6060. Humphrey JD. Continuum biomechanics of soft biological tissues. Proceedings of the Royal Society a-Mathematical Physical and Engineering Sciences. 2003;459:3-46. , 6161. Loree HM, Tobias BJ, Gibson LJ, Kamm RD, Small DM, Lee RT. Mechanical properties of model atherosclerotic lesion lipid pools. Atherioscler Thromb. 1994;14:230-4. ].
• Another specific problem relates to the stress conditions of the imaged aneurysm in vivo. It is common to use data measured in diastole to build the models, but it is important to realise that these structures are not fully unloaded at that point and are subject to initial stresses that ought to be accounted for when an accurate analysis is needed. This is not a trivial problem, but strategies have been published to assess the unloaded configuration from data obtained at diastolic pressure [6262. de Putter S, Wolters B, Rutten MCM, Breeuwer M, Gerritsen FA, van de Vosse FN. Patient-specific initial wall stress in abdominal aortic aneurysms with a backward incremental method. J Biomech. 2007;40:1081-90. , 6363. Gee MW, Forster C, Wall WA. A computational strategy for prestressing patient-specific biomechanical problems under finite deformation. International Journal for Numerical Methods in Biomedical Engineering. 2010;26:52-72. , 6464. Gee MW, Reeps C, Eckstein HH, Wall WA. Prestressing in finite deformation abdominal aortic aneurysm simulation. J Biomech. 2009;42:1732-9. , 6565. Speelman L, Bosboom EMH, Schurink GWH, Buth J, Breeuwer M, Jacobs MJ, van de Vosse FN. Initial stress and nonlinear material behavior in patient-specific AAA wall stress analysis. J Biomech. 2009;42:1713-9. ].
• In addition, arteries exhibit what is called “residual stresses”. These are stresses which are present within the tissue even in fully unloaded arteries, and which are easily visualised by cutting open arterial segmental rings. When residual stresses are present, these rings will open up to a certain opening angle. Nevertheless, it can be anticipated that the order of magnitude of these residual stresses is much lower than of the initial stresses.
• It has been demonstrated that the presence of a thrombus has an effect on wall mechanics, but the magnitude of this effect is highly dependent on assumptions regarding, for example, the permeability and mechanical properties of the thrombus.
• Computational models often analyse isolated arterial segments, but, in reality, these are embedded in and connected to other tissues, most likely interacting with the deformation and stress patterns.
• Computational models require boundary conditions that will interfere with the solution. It is therefore important to impose realistic boundary conditions tailored to the specific situation of the patient.

The above only refers to the computation of the wall stress. In order to assess the risk of rupture of an aneurysm, it is as important to know the ultimate strength of the tissue. Again, overall, there is relatively limited data available. Most studies make use of the statistics-derived multiple linear regression model of Van de Geest et al [5656. Vande Geest JP, Wang DHJ, Wisniewski SR, Makaroun MS, Vorp DA. Towards a noninvasive method for determination of patient-specific wall strength distribution in abdominal aortic aneurysms. Ann Biomed Eng. 2006;34:1098-106. ], where local tissue strength is estimated from a number of clinical patient-related parameters, geometrical information on the aneurysm and the presence of a thrombus. With an estimate of local stress and strength it is possible to calculate the so-called rupture potential index and map it over the aneurysm. There is some evidence from data in patients with ruptured aneurysms that the location of the rupture does coincide with the locations of the highest stresses indicated by stress analysis [6666. Geest JPV, Di Martino ES, Bohra A, Makaroun MS, Vorp DA. A biomechanics-based rupture potential index for abdominal aortic aneurysm risk assessment – Demonstrative application, in Abdominal Aortic Aneurysm: Genetics, Pathophysiology and Molecular Biology, MD Tilson, H Kuivaniemi and GR Upchurch, Editors. 2006. p. 11-21. , 6767. Maier A, Gee MW, Reeps C, Pongratz J, Eckstein HH, Wall WA. A Comparison of Diameter, Wall Stress, and Rupture Potential Index for Abdominal Aortic Aneurysm Rupture Risk Prediction. Ann Biomed Eng. 2010;38:3124-34. , 6868. Xenos M, Rambhia SH, Alemu Y, Einav S, Labropoulos N, Tassiopoulos A, Ricotta JJ, Bluestein D. Patient-Based Abdominal Aortic Aneurysm Rupture Risk Prediction with Fluid Structure Interaction Modeling. Ann Biomed Eng. 2010;38:3323-37. ].

Whether stress analysis in the setting of aneurysms is of clinical use is, however, a question that is extremely hard to assess, and it would require longitudinal patient studies where the decision to intervene would be solely based on the computational analysis. It will be extremely hard to persuade the clinical community and ethics committees to delay an intervention in large aneurysms knowing that failure to predict rupture almost inevitably leads to the loss of a patient. Speeding up an intervention in small aneurysms based on biomechanical grounds may, on the other hand, prevent early ruptures and save lives, but may also lead to unnecessary interventions, exposing patients to the risks related to a surgical intervention they might not need. The only way out of this “catch-22” situation are well controlled studies in animal models which are sufficiently representative of the aneurysmal pathology in humans.

Assessment of plaque vulnerability

Many of the arguments and problems listed above also apply to other problems such as in the assessment of stress in coronary plaques. Here also, the key issue is to know the risk of rupture or the degree of vulnerability of the plaque to identify those plaques that should be treated. Again, the major difficulties arise from a lack of knowledge of accurate 3D geometry, the patient-specific and plaque-specific material characteristics etc. As mentioned elsewhere in this chapter and book, the good news here is that there are high-resolution imaging techniques such as IVUS and intravascular optical coherence tomography (OCT) that do provide accurate geometrical information on the coronary plaque and arterial wall, and might provide a clue about the constituents of the plaque. The disadvantage, however, is that these are invasive techniques, and the information on the vulnerability of the plaque should preferably be known at the moment of intervention. Note that this is somewhat different for carotid plaques, where non-invasive imaging techniques such as MRI and ultrasound can provide the required geometrical information, although with the limitation that the former technique might not be accurate enough to provide the thickness of thin caps, while the latter is hampered by the persisting 2D nature of linear array probes used for vascular diagnosis, and the intrinsic difficulty of measuring calcified tissues with ultrasound [6969. Steinman DA, Thomas JB, Ladak HM, Milner JS, Rutt BK, Spence JD. Reconstruction of carotid bifurcation hemodynamics and wall thickness using computational fluid dynamics and MRI. Magn Reson Med. 2002;47:149-59. , 7070. Zhao SZ, Ariff B, Long Q, Hughes AD, Thom SA, Stanton AV, Xu XY. Inter-individual variations in wall shear stress and mechanical stress distributions at the carotid artery bifurcation of healthy humans. J Biomech. 2002;35:1367-77. ].

Nevertheless, the feasibility of performing computational stress analysis on plaques has been demonstrated both for carotid as well as coronary plaques [7171. Tang DL, Yang C, Zheng J, Woodard PK, Sicard GA, Saffitz JE, Yuan C. 3D MRI-based multicomponent FSI models for atherosclerotic plaques. Ann Biomed Eng. 2004;32:947-60. , 7272. Yang C, Bach RG, Zheng J, Naqa IE, Woodard PK, Teng ZZ, Billiar K, Tang DL. In vivo IVUS-based 3-D fluid-structure interaction models with cyclic bending and anisotropic vessel properties for human atherosclerotic coronary plaque mechanical analysis. IEE Trans Biomed Eng. 2009;56:2420-8. ]. However, overall, the practical usability of the results is still fairly limited, and results have mainly allowed us to gain insight into the relation between plaque stresses and some morphological features of the plaque such as the lipid pool and thin fibrous cap.

Assessment of stent-vessel interaction

In addition to studying the vessel wall stress state under physiological conditions (e.g., to monitor potential disease progression), finite element simulations can also be used to study the biomechanics of minimally invasive medical devices, such as stents and stent grafts as well as their interaction with surrounding tissues ( Figure 13 and Figure 14 ). The application of such a numerical approach in this specific
biomechanical research domain is quite recent and has undergone an enormous evolution over the last few years, as summarised by De Beule [7373. De Beule M. Finite element stent design. PhD thesis, Ghent University, Belgium, 2008. ]. Undoubtedly, all published studies have contributed to the current level of understanding the mechanics of both stent design and angioplasty procedures, and the quality of these studies should be evaluated, taking into account the available knowledge and computational facilities existing at the moment of their publication. In the early years, finite element based studies were primarily focusing on the engineering aspects of the device designs and investigating basic stent characteristics such as elastic recoil, foreshortening, flexibility, radial strength, “dogboning”, etc. Over the years, the models became more realistic by including, for example, the folding pattern of the balloon (see Figure 15 ) and by replacing simplified symmetrical stenosed blood vessel models by more complex patient-specific models [7474. Auricchio F, Di Loreto M, Sacco E. Finite element analysis of a stenotic artery revascularization through a stent insertion. Computer Methods in Biomechanics and Biomedical Engineering. 2001;4:249-63. , 7575. Holzapfel GA, Schulze-Bauer CAJ, Stadler M, Mechanics of angioplasty: Wall, balloon and stent, in Mechanics in Biology, J Casey and G Bao, Editors. 2000: New York. p. 141-156. , 7676. Migliavacca F, Petrini L, Colombo M, Auricchio F, Pietrabissa R. Mechanical behavior of coronary stents investigated through the finite element method. J Biomech. 2002;35:803-11. , 7777. Timmins LH, Moreno MR, Meyer CA, Criscione JC, Rachev A, Moore JE. Stented artery biomechanics and device design optimization. Med Bio Eng Comput. 2007;45:505-13. , 7878. De Beule M, Mortier P, Carlier SG, Verhegghe B, Van Impe R, Verdonck P. Realistic finite element-based stent design: The impact of balloon folding. J Biomech. 2008;41:383-9. , 7979. De Beule M, Van Cauter S, Mortier P, Van Loo D, Van Impe R, Verdonck P, Verhegghe B. Virtual optimization of self-expandable braided wire stents. Med Eng Phys. 2009;31:448-53. , 8080. Mortier P, Holzapfel GA, De Beule M, Van Loo D, Taeymans Y, Segers P, Verdonck P, Verhegghe B. A novel simulation strategy for stent insertion and deployment in curved coronary bifurcations: Comparison of three drug-eluting stents. Ann Biomed Eng. 2010;38:88-99.
This papers illustrates how computational models can be used to investigate the mechanical interaction between different coronary stent designs and a patient-based coronary artery model., 8181. Bedoya J, Meyer CA, Timmins LH, Moreno MR, Moore JE. Effects of stent design parameters on normal artery wall mechanics. J Biomech Eng. 2006;128:757-65. , 8282. Wu W, Yang DZ, Huang YY, Qi M, Wang WQ. Topology optimization of a novel stent platform with drug reservoirs. Med Eng Phys. 2008;30:1177-85. , 8383. Mortier P, Computer modelling of coronary bifurcation stenting, 2010, Ghent University: Ghent, Belgium. ]. This latest evolution has led finite element based simulations from being a basic engineering design tool towards becoming a virtual bench-testing environment for testing clinically relevant hypotheses. The complementarity of virtual bench testing with in vitro experimental bench testing has been reviewed recently by Mortier et al for coronary bifurcation stenting [8484. Mortier P, De Beule M, Dubini G, Hikichi Y, Murasato Y, Ormiston JA. Coronary bifurcation stenting: insights from in vitro and virtual bench testing. Eurointervention. 2010;6:J53-J60. ]. To illustrate the potential of virtual bench testing, three recently published, clinically relevant, finite element supported studies are summarised below.

Timmins at al hypothesised that stents that induce higher mechanical stresses on the artery wall lead to a more aggressive pathobiological response, as determined by the amount of neointimal hyperplasia [8585. Timmins LH, Miller MW, Clubb FJ, Moore JE. Increased artery wall stress post-stenting leads to greater intimal thickening. Lab Invest. 2011;91:955-67. ]. The aim of the study was to examine the role of solid biomechanics in the development of restenosis. A combination of finite element simulations and in vivo analysis were employed to investigate the response to two stent designs that impose greater or lesser levels of stress on the artery wall. Both stent designs were implanted in a porcine model for approximately 28 days and novel integrative pathology techniques (quantitative micro-computed tomography, histomorphometry) were utilised to quantify the pathobiological response. Concomitantly, computer simulations were used to quantify the mechanical loads that the two stents place on the artery. Results revealed a strong correlation between the computed stress values induced on the artery wall and the pathobiological response; the stent that subjected the artery to the higher stresses had significantly more neointimal thickening at stent struts. Therefore, the authors concluded that these differences are a direct result of the solid biomechanical environment, confirming the hypothesis that stents that impose higher wall stresses will provoke a more aggressive pathobiological response. The study provides valuable insight into the role that biomechanics can play in the development of neointimal tissue following vascular stent implantation. However, before generalising the findings and extrapolating them to humans, the study limitations should be addressed and more complex “patient-specific” computational models should be used.

A second clinically relevant study focussing on stent malapposition was published recently by Mortier and colleagues [8686. Mortier P, van Beusekom HM, De Beule M, Krabbendam-Peters I, Van Der Smissen B, De Santis G, Ligthart JM, Verhegghe B, van der Giessen W. Improved understanding of stent malapposition using virtual bench testing. Interventional Cardiology. 2011;6:4. ]. In this study, a novel finite element based approach was used to study the phenomenon of incomplete stent apposition (ISA). This virtual strut apposition assessment technique was employed in the setting of coronary bifurcation stenting and compared simulated strut-artery distances of two stent designs with actual measurements based on optical coherence tomography (OCT) imaging using a silicone model. Stenting of the main branch led to malapposed struts in the proximal part, and the average strut-artery distance in that region for the Integrity stent (Medtronic, Minneapolis, MN, USA) was 126 μm based on the simulation and 117 ± 14 μm based on the OCT analysis. For the Multi-Link 8 stent (Abbott Laboratories. Abbott Park, IL, USA), this average distance is 150 μm and 174±7 μm for the simulation and the in vitro OCT measurements respectively. The study concluded that the virtual assessment of strut appositioning resulted in similar strut-artery distances when compared with measurements based on OCT-visualised in vitro stent deployments and could be used to optimise devices and procedures. The authors suggest that it would be valuable to obtain this kind of highly detailed strut apposition measurement when treating real patients, and one approach would be to base the simulations on pre-operative patient images (e.g., CT combined with IVUS or OCT to gain a higher resolution). This approach is ambitious, and one has to keep in mind that the predictive power of these simulations for real patient treatment still needs to be proven.

A third study indicating the potential of finite element simulations in a clinical setting was published recently by Foin and colleagues [8787. Foin N, Torii R, Mortier P, De Beule M, Viceconti N, Xu Y, Krams R, Di Mario C. Kissing balloon or sequential dilatation of the side branch and main vessel for provisional stenting of bifurcations: Lessons from micro-CT and computational simulations. JACC Cardiovasc Interv. 2012;5:47-56. ]. This in vitro study focused on post-dilatation techniques for coronary bifurcation stenting challenging the kissing balloon (KB) technique with a novel sequential two step post-dilatation of the side branch (SB) and main vessel (MV) without kissing. A series of drug-eluting stents (n = 26) were deployed as main vessel stents in a coronary bifurcation model. Stent apposition and ostial area were quantified from micro-CT scans after both post-dilatation strategies. Vessel wall stresses and detailed reconstruction of blood flow patterns representative of each sequence were obtained using finite element and computational fluid dynamics simulations. KB was shown to create a significant elliptical overexpansion of the MV lumen, inducing higher stress concentration proximal to the SB. KB technique also led to a higher risk of incomplete stent apposition at the proximal stent edge as compared to the 2-step sequence. This study, combining in vitro tests with computational models, led the authors to conclude that sequential 2-step post-dilatation of the SB and MV may offer a simpler and more efficient alternative to final KB technique for provisional stenting of bifurcations.

Limitations of computational models

It should be noted, however, that in several studies there has been a lack of experimental evidence for the obtained numerical results, creating a missing link to reality, and thus provoking an understandable scepticism with respect to numerical models and to the conclusions drawn from them. Such computer models are based on numerous assumptions, and this logically raises questions about the clinical utility of the simulation results. Therefore, considerable effort should be put into the validation of these numerical models using experimental (in vitro and in vivo) data. The small sizes of the typical dimensions of these devices make experimental testing a not altogether trivial undertaking, though currently available and rapidly evolving imaging modalities (such as micro-CT and OCT) have the potential to overcome these challenges [8585. Timmins LH, Miller MW, Clubb FJ, Moore JE. Increased artery wall stress post-stenting leads to greater intimal thickening. Lab Invest. 2011;91:955-67. , 8686. Mortier P, van Beusekom HM, De Beule M, Krabbendam-Peters I, Van Der Smissen B, De Santis G, Ligthart JM, Verhegghe B, van der Giessen W. Improved understanding of stent malapposition using virtual bench testing. Interventional Cardiology. 2011;6:4. , 8787. Foin N, Torii R, Mortier P, De Beule M, Viceconti N, Xu Y, Krams R, Di Mario C. Kissing balloon or sequential dilatation of the side branch and main vessel for provisional stenting of bifurcations: Lessons from micro-CT and computational simulations. JACC Cardiovasc Interv. 2012;5:47-56. ]. When the performed validation is merely qualitative, it might not always be applicable to fully interpret and verify the numerical results, and therefore quantitative validation is vital. The consistent quantitative validation regarding the stent free expansion from De Beule et al [7878. De Beule M, Mortier P, Carlier SG, Verhegghe B, Van Impe R, Verdonck P. Realistic finite element-based stent design: The impact of balloon folding. J Biomech. 2008;41:383-9. ], has shown, for example, that including the folding pattern of the balloon is essential to accurately study stent expansion behaviour. Regarding the vascular reaction to stent deployment, it should be nuanced that measuring – during stent induced expansion – the stresses in the vessel wall in an experimental setup is practically impossible. For such specific numerical studies, it makes sense to compare the results with clinical findings in literature (e.g., restenosis rates) and/or to set up dedicated animal trials. Nevertheless, attention should be paid to the adopted methodology of the cited clinical trials (i.e., investigated stent designs and patient recruitment), and specifically designed new clinical follow-up’s could be required for thorough validation of the developed hypotheses from the numerical results. In addition, it should, however, be feasible to examine the deployment characteristics of a stent using for example micro-CT and/or OCT. Furthermore, the impact of the assumptions that were made (e.g., deployment simulation strategy and applied constitutive material models) on the obtained results should be investigated thoroughly, as already indicated De Beule et al [7878. De Beule M, Mortier P, Carlier SG, Verhegghe B, Van Impe R, Verdonck P. Realistic finite element-based stent design: The impact of balloon folding. J Biomech. 2008;41:383-9. ] and by Holzapfel et al [8888. Holzapfel GA, Stadler M, Schulze-Bauer CAJ. A layerspecific three-dimensional model for the simulation of balloon angioplasty using magnetic resonance imaging and mechanical testing. Ann Biomed Eng. 2002;30:753-67. ].

Advantages of computational models

Complementary to experimental studies, these computational models have proven to be an excellent research tool to optimise the mechanical properties of a stent, especially when physical test methods are difficult or even impossible to implement (e.g., due to implant size, cost). Therefore, numerical simulations may sometimes be the only alternative. The main advantage of numerical modelling are those numerous “What if?” scenarios addressing different materials and designs that can easily be tested and evaluated before devices are actually manufactured. Consequently, the design can be evaluated a priori in terms of radial strength, flexibility, scaffolding properties, etc. which shortens the design process and undoubtedly influences the cost in a favourable way. In addition to the important information revealed by the computer model in the stent design phase, these computational models are also useful to compare different existing designs from different manufacturers. This use of simulations can be defined as virtual bench testing. Subjecting stents to exactly the same virtual tests offers both engineers and physicians an objective comparison of the performance of the investigated designs. In addition to the investigation of coronary stents, these numerical simulations can also be used to study other minimally invasive medical devices such as self-expandable peripheral stents [8989. Auricchio F, Conti M, de Beule M, de Santis G, Verhegghe B. Carotid artery stenting simulation: From patient-specific images to finite element analysis. Med Eng Phys. 2010. , 9090. Early M, Lally C, Prendergast P, Kelly D. Stresses in peripheral arteries following stent placement: a finite element analysis. Comput Methods Biomech Biomed Engin. 2009;12:25-33. ] and embolic protection devices [9191. Conti M, De Beule M, Mortier P, Van Loo D, Verdonck P, Vermassen F, Segers P, Auricchio F, Verhegghe B. Nitinol embolic protection filters: design investigation by finite element analysis. Journal of Materials Engineering and Performance. 2009;18:787-92. ], stented heart valves [9292. Schievano S, Capelli C, Taylor AM, Bonhoeffer P. Application of computational simulations for percutaneous pulmonary valve implantation: Percutaneous pulmonary valve computer analysis. Progress in Pediatric Cardiology. 2010;30:15-21. ], etc. As stated above, to date the use of these numerical models has been mainly proven for the design and mechanical characterisation of stents. However, given the proof-of-concept study from Mortier et al [8080. Mortier P, Holzapfel GA, De Beule M, Van Loo D, Taeymans Y, Segers P, Verdonck P, Verhegghe B. A novel simulation strategy for stent insertion and deployment in curved coronary bifurcations: Comparison of three drug-eluting stents. Ann Biomed Eng. 2010;38:88-99.
This papers illustrates how computational models can be used to investigate the mechanical interaction between different coronary stent designs and a patient-based coronary artery model.], nowadays the interaction with patient-specific vessel models is feasible as discussed in the next paragraph.

Future applications

Future developments in stent modelling will most likely include further integration of innovative stent designs and materials in realistic patient-specific stenosis models. Such integrated models may even have a more important role to play in the stent design phase, eventually entering clinical practice to optimise the coronary revascularisation procedure for a specific patient as a pre-surgical planning tool.

In the search for the ideal stent, new stent materials (e.g., platinum-chromium, superelastic shape-memory alloys, biodegradable polymers, magnesium, etc.) are emerging. Each of these materials has a specific constitutive behaviour, and consequently requires a specific innovative stent design. These new stent designs and materials can and will be further tested and evaluated using computational modelling.

The ongoing (r)evolution in medical imaging providing scientists with even more detailed and accurate geometrical information for the vessel wall and plaque architecture, in combination with new insights in the constitutive material behaviour of soft biological tissues and calcifications, will allow further optimisation of patient-specific modelling strategies. In addition, the recent advances in both image reconstruction, allowing us to transfer these detailed medical images and material data into accurate mathematical models, and simulation tools will only speed-up this optimisation. This patient-specific modelling approach will allow us to gain insights into the actual real-life mechanics of the stents as well as their surrounding tissues and might help, for example, to: (i) formulate design guidelines on how to further reduce the risk of stent fracture [9393. Foerst J, Ball T, Kaplan A. Postmortem in situ micro-CT evaluation of coronary stent fracture. Catheter Cardiovasc Interv. 2010;76:527-31. ] and (ii) develop virtual trials that provide additional evidence that supports and explains the findings of animal and clinical trials. Furthermore, validation of these numerical results with innovative targeted experiments will only encourage the use of computational models. Therefore, the idea of a surgeon implanting a patient specific stent, selected by means of a numerical pre-surgical planning tool, no longer seems like science fiction.

Required research

To be able to reach these above mentioned ambitious future goals, by far the most crucial requirement is extensive model validation. This validation will have to be performed on different levels, mainly on a material level, on a simulation strategy level and on a feasibility level. On a material level, the validity of the constitutive models of both the stent delivery system and the patient-specific target lesion needs to be further proven. This will require additional experimental data collection and numerical implementation/calibration, especially including aspects of micro-fracture mechanics. On a simulation strategy level, further validation of the modelling assumptions is required. Numerical simulations will always be approximations of the physical reality, though well-chosen and validated assumptions will allow us to approach the real physical conditions as close as possible. An acceptable level of accuracy can only be reached by an extensive comparison of the simulation results with in vitro and in vivo data. As an example, the resulting stent deformations after implantation can be compared with dedicated in vitro bench tests and in vivo 3D imaging modalities (e.g., IVUS, OCT) [8686. Mortier P, van Beusekom HM, De Beule M, Krabbendam-Peters I, Van Der Smissen B, De Santis G, Ligthart JM, Verhegghe B, van der Giessen W. Improved understanding of stent malapposition using virtual bench testing. Interventional Cardiology. 2011;6:4. ]. Additionally, further advances in strain imaging might allow us to validate the numerically predicted strain values. Finally, after proper model validation, the feasibility of using this technology on a large scale for virtual trials and/or pre-surgical planning still needs to be demonstrated. This will, without doubt, require dedicated tools to automate and speed-up these simulations, as well as commitments from the clinical community. Furthermore, future modelling will certainly be comprised of an integrated approach combining a profound study of the fluid dynamic aspects and vascular biological response of, for instance, interventional procedures. To examine the predictive capacity of these numerical simulations, targeted animal and/or clinical trials will presumably be an essential condition.

Shear stress in clinical studies

In one of the first studies that employed the ANGUS method, Krams et al [2424. Krams R, Wentzel J, Oomen J, Vinke R, Schuurbiers J, de Feyter P, Serruys P, Slager C. Evaluation of endothelial shear stress and 3D geometry as factors determining the development of atherosclerosis and remodeling in human coronary arteries in vivo. Combining 3D reconstruction from angiography and IVUS (ANGUS) with computational fluid dynamics. Arterioscler Thromb Vasc Biol. 1997;17:2061-5. ] investigated the relationship between shear stress and vessel wall thickness in the right coronary artery. Data on vessel wall thickness were derived from IVUS and considered as a marker for the presence of an atherosclerotic plaque. They demonstrated an inverse relationship between shear stress and wall thickness: thicker plaques were observed in regions exposed to the lowest shear stress.

This observation was confirmed by the work from Stone et al [2525. Stone PH, Coskun AU, Kinlay S, Clark ME, Sonka M, Wahle A, Ilegbusi OJ, Yeghiazarians Y, Popma JJ, Orav J, Kuntz RE, Feldman CL. Effect of endothelial shear stress on the progression of coronary artery disease, vascular remodeling, and in-stent restenosis in humans: in vivo 6-month follow-up study. Circulation. 2003;108:438-44. ] who studied plaque localisation and progression over a 6 month period. They demonstrated that regions exposed to low shear stress at baseline present with a significant increase in wall thickness. This increase in wall thickness was accompanied by an increase in the external elastic membrane dimensions such that lumen dimensions remained unaltered. Regions exposed to higher shear stress additionally underwent outward remodelling leading to a normalisation of shear stress values.

Wentzel et al [2626. Wentzel JJ, Janssen E, Vos J, Schuurbiers JC, Krams R, Serruys PW, de Feyter PJ, Slager CJ. Extension of increased atherosclerotic wall thickness into high shear stress regions is associated with loss of compensatory remodeling. Circulation. 2003;108:17-23. ] investigated the relationship between shear stress and wall thickness in the angiographically normal segments of human coronary arteries of 14 patients. Based on the area stenosis, the segments were divided into segments with lumen preservation and segments with lumen narrowing. The previously reported inverse relationship was observed for the segments with lumen preservation, however, not for the segments with lumen narrowing, indicating that the processes related to protrusion of the plaque into the lumen are not regulated by shear stress.

Instead of using IVUS derived wall thickness data as a marker for atherosclerosis, one can use other imaging parameters as well. Gijsen et al [2727. Gijsen FJH, Wentzel JJ, Thury A, Mastik F, Schaar JA, Schuurbiers JCH, Slager CJ, van der Giessen WJ, de Feyter PJ, van der Steen AFW, Serruys PW. Strain distribution over plaques in human coronary arteries relates to shear stress. American Journal of Physiology - Heart and Circulatory Physiology. 2008;295:H1608-14. ] applied an intravascular ultrasound technique, called palpography (see also section “How can we measure vessel wall strain”), that can measure the strain distribution in the vessel wall layer adjacent to the lumen. Strain can be considered as a surrogate marker for plaque composition. Ex vivo experiments have shown that high strain values are associated with increased macrophage accumulation, low smooth muscle cell content and thin fibrous caps. In contrast, low strain values indicate the presence of stiff wall material and are related to high smooth muscle cell content. In 13 coronary arteries, 31 plaques were identified. These plaques were divided into 4 regions: the upstream, midcap, downstream and shoulder region. The downstream region was exposed to low shear stress, and strain values were lower there, indicating that more smooth muscle cells are present downstream of a plaque. The other regions could not be separated based on shear stress or strain values. However, plaque regions exposed to the highest shear stress levels revealed the highest strain, indicating that those regions are weaker. In a subset of this patient group, 6 month follow-up strain data was available as well [2828. Gijsen FJ, Mastik F, Schaar JA, Schuurbiers JC, van der Giessen WJ, de Feyter PJ, Serruys PW, van der Steen AF, Wentzel JJ. High shear stress induces a strain increase in human coronary plaques over a 6-month period. EuroIntervention. 2001;7:121-7. ]. It was seen that regions exposed to the highest shear stress showed an increase of strain, suggesting that those plaque regions got weaker over time. These results imply that high shear stress might induce patho-biological responses in the more advanced phases of atherosclerosis that lead to enhanced plaque vulnerability.

These findings are in keeping with another study in which the relationship between shear stress and plaque composition derived from virtual histology intravascular ultrasound was investigated [2929. Samady H, Eshtehardi P, McDaniel MC, Suo J, Dhawan SS, Maynard C, Timmins LH, Quyyumi AA, Giddens DP. Coronary artery wall shear stress is associated with progression and transformation of atherosclerotic plaque and arterial remodeling in patients with coronary artery disease. Circulation. 2011;124:779-88. ]. It was observed that plaque regions exposed to low shear stress showed an increase of plaque area over a 6-month period, with a significant increase in necrotic core area. The high shear stress regions demonstrated a decrease in plaque area, which was associated with an increase in necrotic core region and a regression of fibrous and fibrofatty tissue components, suggesting that the high shear stress regions are more vulnerable.

Rupture of the vulnerable plaque can lead to events and therefore represents the most relevant phase of atherosclerosis for the patient. Rupture occurs at the location where the cap is the weakest, and the previously discussed studies indicate that shear stress might be one of the factors that influences cap strength. High shear stress might be involved in various processes that locally increase vulnerability, a finding that was confirmed in two recent studies. Fukumoto et al [3030. Fukumoto Y, Hiro T, Fujii T, Hashimoto G, Fujimura T, Yamada J, Okamura T, Matsuzaki M. Localized elevation of shear stress is related to coronary plaque rupture: a 3-dimensional intravascular ultrasound study with in-vivo color mapping of shear stress distribution. J Am Coll Cardiol. 2008;51:645-50. ] applied IVUS to determine the location of plaque rupture in culprit lesions. They qualitatively associated the location of plaque rupture in the lumen narrowing lesions with locally elevated shear stress levels. They demonstrated that the location of plaque rupture was found predominantly in the upstream shoulder regions and that the rupture location was, on average, exposed to higher shear stress levels than the plaque. A similar study was performed by Gijsen et al, who quantitatively assessed the shear stress at the location of plaque ulcers by finite element modelling in 3D reconstructed human coronary arteries. Comparison of shear stress at the ulcer location with the plaque and healthy wall locations confirmed higher shear stress at the ulcer location [9494. Gijsen FJ, Schuurbiers JC, van de Giessen AG, Schaap M, van der Steen AF, Wentzel JJ. 3D reconstruction techniques of human coronary bifurcations for shear stress computations.J Biomech. 2014 Jan 3;47(1):39-43. doi: 10.1016/j.jbiomech.2013.10.021. Epub 2013 Oct 22. ].

Shear stress was also investigated in a number of studies for its power to predict culprit lesions leading to cardiovascular events. Since both low and high shear stress proved to be involved in plaque generation, destabilization and rupture, both low and high shear stress were studied in patients that presented with cardiovascular events in the follow up period. For that purpose Stone et al assessed shear stress using imaging data from the Prospect study, a natural history study on plaque progression and destabilization using multi-modality serial invasive imaging [9595. Stone GW, Maehara A, Lansky AJ, de Bruyne B, Cristea E, Mintz GS, Mehran R, McPherson J, Farhat N, Marso SP, Parise H, Templin B, White R, Zhang Z, Serruys PW; PROSPECT Investigators. A prospective natural-history study of coronary atherosclerosis. N Engl J Med. 2011;364:226-35. , 9696. Stone PH, Maehara A, Coskun AU, Maynard CC, Zaromytidou M, Siasos G, Andreou I, Fotiadis D, Stefanou K, Papafaklis M, Michalis L, Lansky AJ, Mintz GS, Serruys PW, Feldman CL, Stone GW. Role of Low Endothelial Shear Stress and Plaque Characteristics in the Prediction of Nonculprit Major Adverse Cardiac Events: The PROSPECT Study. JACC Cardiovasc Imaging. 2018;1:462-471. ]. That study showed in 23 culprit segments that low shear stress in a culprit segment was significantly lower than in the 122 control segments. Shear stress lower than 1.3 Pa, often located proximal or distal of the plaque, was associated with a culprit lesion with a hazard ratio of 4.34 [9696. Stone PH, Maehara A, Coskun AU, Maynard CC, Zaromytidou M, Siasos G, Andreou I, Fotiadis D, Stefanou K, Papafaklis M, Michalis L, Lansky AJ, Mintz GS, Serruys PW, Feldman CL, Stone GW. Role of Low Endothelial Shear Stress and Plaque Characteristics in the Prediction of Nonculprit Major Adverse Cardiac Events: The PROSPECT Study. JACC Cardiovasc Imaging. 2018;1:462-471. ]. In contrast, shear stress analysis in coronary patients from the FAME study using 3D-angiography, demonstrated that high shear stress was the most predictive for vessel related myocardial infarction [9797. Kumar A, Thompson EW, Lefieux A, Molony DS, Davis EL, Chand N, Fournier S, Lee HS, Suh J, Sato K, Ko YA, Molloy D, Chandran K, Hosseini H, Gupta S, Milkas A, Gogas B, Chang HJ, Min JK, Fearon WF, Veneziani A, Giddens DP, King SB 3rd, De Bruyne B, Samady H. High Coronary Shear Stress in Patients With Coronary Artery Disease Predicts Myocardial Infarction. J Am Coll Cardiol. 2018;72:1926-1935. ]. After adjustment for coronary flow reserve, diameter stenosis and lesion length, high shear stress at the proximal side of the plaque remained highly significant. Thus high shear stress was incremental to fractional flow reserve in the prediction of vessel-related-cardiovascular events. More research is needed to isolate the best combination of biomechanical and geometrical predictors of future cardiovascular events.

Shear stress is associated with various markers of atherosclerotic disease not only in untreated arteries but also after stent placement, which was convincingly demonstrated in an animal study by Carlier et al using rabbits [3131. Carlier SG, van Damme LC, Blommerde CP, Wentzel JJ, van Langehove G, Verheye S, Kockx MM, Knaapen MW, Cheng C, Gijsen F, Duncker DJ, Stergiopulos N, Slager CJ, Serruys PW, Krams R. Augmentation of wall shear stress inhibits neointimal hyperplasia after stent implantation: inhibition through reduction of inflammation. Circulation. 2003;107:2741-6. ]. They introduced a stent with a flow divider in the centre in one of the iliac arteries, and a stent without the flow divider in the other iliac artery. The flow divider induced a twofold increase in shear stress in the stent. It was shown that the increased shear stress levels lead to a decrease in neointima hyperplasia and a decrease of inflammation.

Wentzel et al [3232. Wentzel JJ, Krams R, Schuurbiers JC, Oomen JA, Kloet J, van Der Giessen WJ, Serruys PW, Slager CJ. Relationship between neointimal thickness and shear stress after Wallstent implantation in human coronary arteries. Circulation. 2001;103:1740-5. ] used the previously discussed 3D reconstruction technique to investigate the relationship between shear stress and neointima hyperplasia in self-expanding stents in 14 human coronary arteries. They found that after a 6-month period, the neointimal hyperplasia was more profound in the low shear stress regions. These findings were not confirmed by Stone et al for balloon-expandable stents in a smaller patient population [2525. Stone PH, Coskun AU, Kinlay S, Clark ME, Sonka M, Wahle A, Ilegbusi OJ, Yeghiazarians Y, Popma JJ, Orav J, Kuntz RE, Feldman CL. Effect of endothelial shear stress on the progression of coronary artery disease, vascular remodeling, and in-stent restenosis in humans: in vivo 6-month follow-up study. Circulation. 2003;108:438-44. ]. Finally, in drug-eluting stents, an inverse relation between shear stress and neointima thickness was found by Gijsen et al [3333. Gijsen FJ, Oortman RM, Wentzel JJ, Schuurbiers JC, Tanabe K, Degertekin M, Ligthart JM, Thury A, de Feyter PJ, Serruys PW, Slager CJ. Usefulness of shear stress pattern in predicting neointima distribution in sirolimus-eluting stents in coronary arteries. Am J Cardiol. 2003;92:1325-8. ]. In that study it was shown that stent regions exposed to higher shear stress at baseline were associated with tissue regression at 6-month follow-up.

In conclusion, due to the movement of the heart and the size of the coronary arteries, direct non-invasive imaging of shear stress is not currently feasible. Application of invasive 3D imaging to obtain the shape of the coronary in combination with computational methods is the most reliable way to determine shear stress. Using these methods it was shown that shear stress could be associated with various markers of atherosclerosis in human coronary arteries. It was demonstrated that locations exposed to low shear stress are most frequently affected by atherosclerotic disease. Plaques protruding into the lumen are exposed to locally elevated shear stress levels, and these regions are associated with enhanced vulnerability. In segments implanted with stents, decreased shear stress is associated with patterns of in-stent restenosis.

Personal perspective – Frank Gijsen

The field of cardiovascular biomechanics has been transformed dramatically over the last two decades. In the early nineties, hydraulic bench experiments were performed to study biological flow in glass models of idealised geometries using water as a measuring fluid. Experimental evaluation of biomechanical properties of the healthy arterial wall was extremely challenging, and numerical simulation of arterial wall and fluid mechanics was limited to highly simplified systems.
On the experimental side, recent developments in in vitro and in vivo high resolution imaging greatly enhanced our ability to visualise blood flow and relevant vessel wall components as well as their deformation under loading conditions, enabling their mechanical characterisation. From the modelling perspective, the recent advances in computational power and modelling capacities enable us to simulate healthy and diseased vessel wall behaviour under conditions which resemble the physiological environment, thus keeping up with advanced experimental methods. These developments need to go hand-in-hand in order to be able to validate numerical results on the one side, and guide experimental procedures on the other.
Due to these recent developments, biomechanical models were successfully applied in various patient studies, greatly enhancing our understanding of the interaction between shear stress, the endothelium and atherosclerosis. It also proved to be indispensable in optimising the design of devices like balloon-expandable stents.
One can foresee that the combination of rapid developments in noninvasive imaging and the progress in determining the properties of blood and diseased arteries on a per patient basis will set the basis for patient-specific modelling. Tailor-made patient-specific – or rather plaque-specific – solutions for various problems will then be within reach: Do we really need to treat this vessel since shear stress upstream might weaken this plaque? Is blood pressure really high enough to potentially rupture this specific plaque? What stent design will cause minimal damage to the coronary wall of this patient?
We still need to solve many – non-trivial – problems before we can address these questions adequately, but once they are solved, the fusion of noninvasive imaging and biomechanical modelling will help the cardiologist to improve diagnosis and establish optimal treatment strategies for patients suffering from cardiovascular disease.